题目内容
9.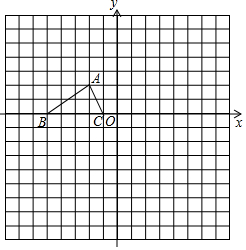 如图,已知△ABC的三个顶点的坐标分别为A(-2,2)、B(-5,0)、C(-1,0),P(a,b)是△ABC的边AC上一点:
如图,已知△ABC的三个顶点的坐标分别为A(-2,2)、B(-5,0)、C(-1,0),P(a,b)是△ABC的边AC上一点:(1)将△ABC绕原点O逆时针旋转90°得到△A1B1C1,请在网格中画出△A1B1C1,旋转过程中点A所走的路径长为 $\sqrt{2}$π.
(2)将△ABC沿一定的方向平移后,点P的对应点为P2(a+6,b+2),请在网格画出上述平移后的△A2B2C2,并写出点A2的坐标:A2(4,4).
(3)若以点O为位似中心,作△A3B3C3与△ABC成2:1的位似,则与点P对应的点P3位似坐标为(2a,2b)或(-2a,-2b)(直接写出结果).
分析 (1)将点A、B、C分别绕原点O逆时针旋转90°得到对应点,顺次连接即可得,根据弧长公式求解路径长;
(2)根据点P的对应点得出平移方向和距离,根据平移的定义画出点A、B、C的对应点A2、B2、C2,从而得到△A2B2C2;
(3)把点P的横纵坐标都乘以2或-2得到P3的坐标,然后描点即可.
解答 解:(1)如图,△A1B1C1即为所求三角形,
∵OA=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∴旋转过程中点A所走的路径长为$\frac{90•π•2\sqrt{2}}{180}$=$\sqrt{2}$π,
故答案为:$\sqrt{2}$π;
(2)如图,△A2B2C2即为所求三角形,点A2的坐标为(4,4),
故答案为:(4,4);
(3)由位似变换性质可知P3(2a,2b)或P3(-2a,-2b),
故答案为:(2a,2b)或(-2a,-2b).
点评 本题主要考查作图-位似变换、平移变换、旋转变换,熟练掌握基本变换的定义和性质是解题的关键.

练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
19. 一个几何体由n个大小相同的小正方体搭成,其左视图、俯视图如图所示,则n的最小值是( )
一个几何体由n个大小相同的小正方体搭成,其左视图、俯视图如图所示,则n的最小值是( )
 一个几何体由n个大小相同的小正方体搭成,其左视图、俯视图如图所示,则n的最小值是( )
一个几何体由n个大小相同的小正方体搭成,其左视图、俯视图如图所示,则n的最小值是( )| A. | 5 | B. | 7 | C. | 9 | D. | 10 |
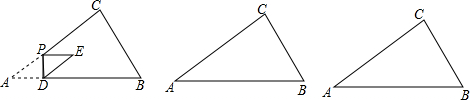
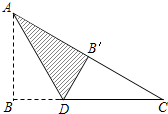 如图,Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在斜边AC上,与点B′重合,AD为折痕,求DB′的长.
如图,Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在斜边AC上,与点B′重合,AD为折痕,求DB′的长.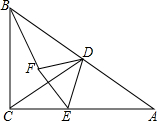 如图,在Rt△ABC中,∠C=90°,∠A=30°.点D是AB中点,点E为边AC上一点,连接CD,DE,以DE为边在DE的左侧作等边三角形DEF,连接BF.
如图,在Rt△ABC中,∠C=90°,∠A=30°.点D是AB中点,点E为边AC上一点,连接CD,DE,以DE为边在DE的左侧作等边三角形DEF,连接BF. 在江苏卫视《最强大脑》节目中,搭载百度大脑的小度机器人以3:1的总战绩,斩获2017年度脑王巅峰对决的晋级资格,人工智能时代已经扑面而来.
在江苏卫视《最强大脑》节目中,搭载百度大脑的小度机器人以3:1的总战绩,斩获2017年度脑王巅峰对决的晋级资格,人工智能时代已经扑面而来.