题目内容
19．解不等式组：$\left\{\begin{array}{l}{2x+4≤5（x+2）}\\{3x＜\frac{x+7}{2}}\end{array}\right.$．分析 先求出每个不等式的解集，再求出不等式组的解集即可．
解答 解：$\left\{\begin{array}{l}{2x+4≤5（x+2）①}\\{3x＜\frac{x+7}{2}②}\end{array}\right.$
∵由①得：x≥-2，
由②得：x＜$\frac{7}{5}$，
∴不等式组的解是-2≤x＜$\frac{7}{5}$．
点评 本题考查了解一元一次不等式和解一元一次不等式组，能根据不等式的解集找出不等式组的解集是解此题的关键．
练习册系列答案
相关题目
16．
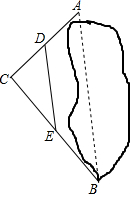如图，要测定被池塘隔开的A，B两点的距离．可以在AB外选一点C，连接AC，BC，并分别找出它们的中点D，E，连接DE．现测得AC=30m，BC=40m，DE=24m，则AB=（ ）
如图，要测定被池塘隔开的A，B两点的距离．可以在AB外选一点C，连接AC，BC，并分别找出它们的中点D，E，连接DE．现测得AC=30m，BC=40m，DE=24m，则AB=（ ）| A． | 50m | B． | 48m | C． | 45m | D． | 35m |
11．
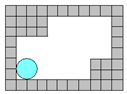将半径为2cm的圆形纸板沿着挖空的部分方格纸板（小方格的边长为2cm）的内侧滚动一周，回到开始位置后，圆心经过的路线的长度为 （ ）（精确到0.01cm）
将半径为2cm的圆形纸板沿着挖空的部分方格纸板（小方格的边长为2cm）的内侧滚动一周，回到开始位置后，圆心经过的路线的长度为 （ ）（精确到0.01cm）| A． | 36cm | B． | 42.28cm | C． | 40.28cm | D． | 40cm |