题目内容
16.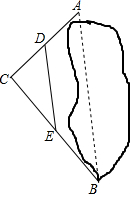 如图,要测定被池塘隔开的A,B两点的距离.可以在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接DE.现测得AC=30m,BC=40m,DE=24m,则AB=( )
如图,要测定被池塘隔开的A,B两点的距离.可以在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接DE.现测得AC=30m,BC=40m,DE=24m,则AB=( )| A. | 50m | B. | 48m | C. | 45m | D. | 35m |
分析 根据中位线定理可得:AB=2DE=48m.
解答 解:∵D是AC的中点,E是BC的中点,
∴DE是△ABC的中位线,
∴DE=$\frac{1}{2}$AB,
∵DE=24m,
∴AB=2DE=48m,
故选B.
点评 本题考查了三角形的中位线定理,属于基础题,熟练掌握三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.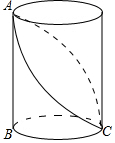 如图,已知圆柱的底面直径BC=$\frac{6}{π}$,高AB=3,小虫在圆柱表面爬行,从C点爬到A点,然后再沿另一面爬回C点,则小虫爬行的最短路程为( )
如图,已知圆柱的底面直径BC=$\frac{6}{π}$,高AB=3,小虫在圆柱表面爬行,从C点爬到A点,然后再沿另一面爬回C点,则小虫爬行的最短路程为( )
 如图,已知圆柱的底面直径BC=$\frac{6}{π}$,高AB=3,小虫在圆柱表面爬行,从C点爬到A点,然后再沿另一面爬回C点,则小虫爬行的最短路程为( )
如图,已知圆柱的底面直径BC=$\frac{6}{π}$,高AB=3,小虫在圆柱表面爬行,从C点爬到A点,然后再沿另一面爬回C点,则小虫爬行的最短路程为( )| A. | $3\sqrt{2}$ | B. | $3\sqrt{5}$ | C. | $6\sqrt{5}$ | D. | $6\sqrt{2}$ |
1.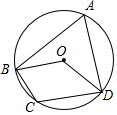 如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则$\widehat{BD}$的长为( )
如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则$\widehat{BD}$的长为( )
 如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则$\widehat{BD}$的长为( )
如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则$\widehat{BD}$的长为( )| A. | π | B. | $\frac{3}{2}π$ | C. | 2π | D. | 3π |
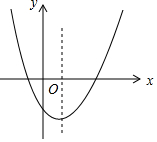 如图,是二次函数y=ax2+bx+c的图象,对下列结论:①ab>0,②abc>0,③$\frac{4ac}{{b}^{2}}$<1,其中错误的个数是( )
如图,是二次函数y=ax2+bx+c的图象,对下列结论:①ab>0,②abc>0,③$\frac{4ac}{{b}^{2}}$<1,其中错误的个数是( )
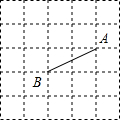 如图,在5×5的正方形网格中有一条线段AB,点A与点B均在格点上.请在这个网格中作线段AB的垂直平分线.要求:①仅用无刻度直尺,且不能用直尺中的直角;②保留必要的作图痕迹.
如图,在5×5的正方形网格中有一条线段AB,点A与点B均在格点上.请在这个网格中作线段AB的垂直平分线.要求:①仅用无刻度直尺,且不能用直尺中的直角;②保留必要的作图痕迹. 如图,图中虚线部分使用围墙材料,其长度为70m,要使围成的矩形面积最大,长和宽分别为35m,35m.
如图,图中虚线部分使用围墙材料,其长度为70m,要使围成的矩形面积最大,长和宽分别为35m,35m.