题目内容
有两堆棋子,第一堆棋子比第二堆棋子数目多,从第一堆棋子中拿出若干粒到第二堆,使第二堆的棋子数翻倍,然后从第二堆中拿出若干粒到第一堆,使第一堆的棋子数翻倍,最后从第一堆中再拿出若干粒到第二堆,使第二堆的棋子数翻倍.此时发现第一堆棋子数与第二堆的棋子数一样多,求原来这两堆棋子的数目最少是多少?
考点:应用类问题
专题:
分析:设第一堆棋子有x颗,第二堆棋子有y颗,根据题意得到第三次变化后二堆棋子的颗数,再根据等量关系:第三次变化后第一堆棋子数与第二堆的棋子数一样多,列出方程,根据棋子是整数x>y即可求解.
解答:解:设第一堆棋子有x颗,第二堆棋子有y颗,
那么第一变化后,第一堆有(x-y)颗,第二堆棋子有2y颗;
第二次变化后,第一堆有2(x-y)颗,第二堆棋子有2y-(x-y)颗;
第三次变化后,第一堆有2(x-y)-[2y-(x-y)]颗,第二堆棋子有2[2y-(x-y)]颗,此时相等,
故(2x-y)-[2y-(x-y)]=2[2y-(x-y)],
解得:5x=11y,
∵棋子是整数x>y,
∴此时是5和11的倍数,即最少的x=11,y=5
那么第一变化后,第一堆有(x-y)颗,第二堆棋子有2y颗;
第二次变化后,第一堆有2(x-y)颗,第二堆棋子有2y-(x-y)颗;
第三次变化后,第一堆有2(x-y)-[2y-(x-y)]颗,第二堆棋子有2[2y-(x-y)]颗,此时相等,
故(2x-y)-[2y-(x-y)]=2[2y-(x-y)],
解得:5x=11y,
∵棋子是整数x>y,
∴此时是5和11的倍数,即最少的x=11,y=5
点评:考查了应用类问题,根据题意得出第三次变化后二堆棋子的颗数,以及根据等量关系得到方程是完成本题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
 小明在画函数y=|x|的图象时,得到了如图甲所示的图象.他发现这个图象好像是把函数y=x的图象x轴下方的部分翻折到x轴上方(如图乙).于是他得出这样的结论:y=|kx+b|的图象都可以这样做,你认为他的结论正确吗?能由y=kx+b的图象得到y=|kx+b|的图象吗?
小明在画函数y=|x|的图象时,得到了如图甲所示的图象.他发现这个图象好像是把函数y=x的图象x轴下方的部分翻折到x轴上方(如图乙).于是他得出这样的结论:y=|kx+b|的图象都可以这样做,你认为他的结论正确吗?能由y=kx+b的图象得到y=|kx+b|的图象吗?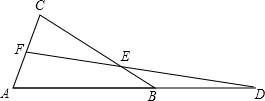 如图,△ABC中,D为AB延长线上一点,E、F分别为BC、AC上一点,已知AF=EB,求证:BC•ED=AC•DF.
如图,△ABC中,D为AB延长线上一点,E、F分别为BC、AC上一点,已知AF=EB,求证:BC•ED=AC•DF.