题目内容
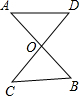如图，AB和CD交于点O，当∠A=∠C时，求证：OA•OB=OC•OD．考点：相似三角形的判定与性质
专题：证明题
分析：运用两个三角形两个角相等，得出△OAD∽△OCB，得到比例式即可得出OA•OB=OC•OD．
解答：解：∵∠A=∠C，∠AOD=∠BOC，
∴△OAD∽△OCB，
∴
=
，
∴OA•OB=OC•OD．
∴△OAD∽△OCB，
∴
| OA |
| OC |
| OD |
| OB |
∴OA•OB=OC•OD．
点评：本题主要考查了相似三角形的判定与性质，解题的关键是得出△OAD∽△OCB．
练习册系列答案
阅读快车系列答案
相关题目
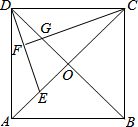如图，已知正方形ABCD中，AC、BD相交于点O，E是OA上一点，CF分别交BD、ED于点G、F，且OG=OE．问CG与DE有怎样的关系？试证明你的结论．（提示：关系有位置关系与数量关系）
如图，已知，?ABCD中，DM，BN都和对角线AC垂直，M，N为垂足．