题目内容
乘法公式的探究及应用.
探究活动:
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,面积是 (写成多项式乘法的形式);
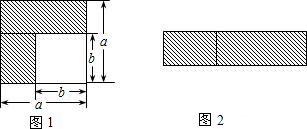
(3)比较图1、图2阴影部分的面积,可以得到公式 ;
知识应用:运用你所得到的公式解决以下问题:
(1)计算:(a+2b-c)(a-2b+c);
(2)若4x2-9y2=10,4x+6y=4,求2x-3y的值.
探究活动:
(1)如图1,可以求出阴影部分的面积是
(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,面积是

(3)比较图1、图2阴影部分的面积,可以得到公式
知识应用:运用你所得到的公式解决以下问题:
(1)计算:(a+2b-c)(a-2b+c);
(2)若4x2-9y2=10,4x+6y=4,求2x-3y的值.
考点:平方差公式的几何背景
专题:
分析:(1)大正方形的面积与小正方形的面积的差就是阴影部分的面积;
(2)利用矩形的面积公式即可求解;
(3)根据(1)(2)表示的阴影部分面积相等即可解答;
知识应用:(1)利用平方差公式即可求解;
(2)4x2-9y2=(2x+3y)(2x-3y),由4x+6y=4得2x+3y=2,代入即可求解.
(2)利用矩形的面积公式即可求解;
(3)根据(1)(2)表示的阴影部分面积相等即可解答;
知识应用:(1)利用平方差公式即可求解;
(2)4x2-9y2=(2x+3y)(2x-3y),由4x+6y=4得2x+3y=2,代入即可求解.
解答:解:(1)阴影部分的面积是:a2-b2,
故答案是:a2-b2;
(2)长方形的面积是(a+b)(a-b),
故答案是:(a+b)(a-b);
(3)可以得到公式:a2-b2=(a+b)(a-b),
故答案是:a2-b2=(a+b)(a-b);
应用:(1)原式=【a+(2b-c)】【a-(2b-c)】
=a2-(2b-c)2
=a2-4b2+4bc-c2;
(2)4x2-9y2=(2x+3y)(2x-3y)=10,
由4x+6y=4得2x+3y=2,
则2(2x-3y)=10,
解得:2x-3y=5.
故答案是:a2-b2;
(2)长方形的面积是(a+b)(a-b),
故答案是:(a+b)(a-b);
(3)可以得到公式:a2-b2=(a+b)(a-b),
故答案是:a2-b2=(a+b)(a-b);
应用:(1)原式=【a+(2b-c)】【a-(2b-c)】
=a2-(2b-c)2
=a2-4b2+4bc-c2;
(2)4x2-9y2=(2x+3y)(2x-3y)=10,
由4x+6y=4得2x+3y=2,
则2(2x-3y)=10,
解得:2x-3y=5.
点评:本题主要考查了平方差公式的几何表示,表示出图形阴影部分面积是解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
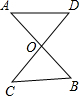 如图,AB和CD交于点O,当∠A=∠C时,求证:OA•OB=OC•OD.
如图,AB和CD交于点O,当∠A=∠C时,求证:OA•OB=OC•OD.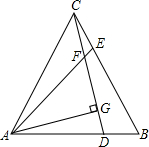 如图,在等边三角形ABC中,D、E分别为AB、BC上的点,且BD=CE,AE、CD相交于点F,AG⊥CD,垂足为G.求证:
如图,在等边三角形ABC中,D、E分别为AB、BC上的点,且BD=CE,AE、CD相交于点F,AG⊥CD,垂足为G.求证: 如图,菱形ABCD中,若BD=24,AC=10,则AB的长等于
如图,菱形ABCD中,若BD=24,AC=10,则AB的长等于