题目内容
如图，已知，?ABCD中，DM，BN都和对角线AC垂直，M，N为垂足．求证：DM=BN．
考点：平行四边形的性质,全等三角形的判定与性质
专题：证明题
分析：根据平行四边形的性质，由AAS证明△ADM≌△CBN，再根据全等三角形的性质即可求解．
解答：证明：∵DM，BN都和对角线AC垂直，
∴∠AMD=∠CNB=90°，
∵在?ABCD中，AD=BC且AD∥BC，
∴∠DAM=∠CBN，
在△ADM与△CBN中，
，
∴△ADM≌△CBN（AAS），
∴DM=BN．
∴∠AMD=∠CNB=90°，
∵在?ABCD中，AD=BC且AD∥BC，
∴∠DAM=∠CBN，
在△ADM与△CBN中，
|
∴△ADM≌△CBN（AAS），
∴DM=BN．
点评：本题考查了利用平行四边形的性质结合三角形全等来解决有关线段相等的证明．
练习册系列答案
相关题目
如图，某海域直径为30海里的暗礁区中心有一哨所A，值班人员发现有一民用轮船从哨所正西方向90海里的B处，以20节的速度（1节=海里1/小时）向哨所驶来，哨所及时向轮船发出了危险信号，但是轮船没有收到信号，该轮船又继续前进了45分钟，到达C处，此时哨所第二次发出了危险新号．当轮船收到第二次信号时，为避免触礁，轮船航向改变角度至少为东偏北α度，则tanα的值为（ ）
如图，已知三角形ABCD中点A（1，2），B（3，5），C（4，3），小张同学在画完图后不小心把坐标轴给擦掉了，请你帮他画出x轴，y轴及原点，并计算三角形ABC的面积．
如图，在?ABCD中，F是AD的中点，延长BC到点E，使CE=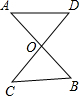
如图，AB和CD交于点O，当∠A=∠C时，求证：OA•OB=OC•OD．