题目内容
18.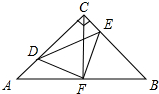 如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB=4,F是AB边上的中点,点D、E分别在AC、BC边上运动(点D不与点A,C重合),且始终保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,有下列结论:
如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB=4,F是AB边上的中点,点D、E分别在AC、BC边上运动(点D不与点A,C重合),且始终保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,有下列结论:(1)△DFE是等腰直角三角形;
(2)四边形CEDF有可能成为正方形;
(3)四边形CEDF的面积随点E的位置的改变而发生变化;
(4)点C到线段DE的最大距离为$\sqrt{2}$.
其中正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 (1)易证△ADF≌△CEF,从而可得FD=FE,∠AFD=∠CFE,即可得到∠DFE=∠AFC=90°,从而可得△DFE是等腰直角三角形.
(2)当FD⊥AC时,易证四边形CEDF是矩形,由FD=FE可得矩形CEDF是正方形;
(3)由△ADF≌△CEF可得S△ADF=S△CEF,从而可得S四边形CEDF=S△AFC=$\frac{1}{2}$S△ABC(定值);
(4)易得当DE⊥CF时,点C到线段DE的距离最大,等于$\frac{1}{2}$CF,只需求出CF,即可解决得到点C到线段DE的最大距离.
解答 解:(1)∵∠ACB=90°,AC=CB=4,F是AB边上的中点,
∴CF=AF=BF,CF⊥AB,
∴∠A=∠B=∠ACF=∠BCF=45°.
在△ADF和△CEF中,
$\left\{\begin{array}{l}{AD=CE}\\{∠A=∠ECF}\\{AF=CF}\end{array}\right.$,
∴△ADF≌△CEF,
∴FD=FE,∠AFD=∠CFE,
∴∠DFE=∠AFC=90°,
∴△DFE是等腰直角三角形.
故(1)正确;
(2)当FD⊥AC时,
∵∠DCE=∠CDF=∠DFE=90°,
∴四边形CEDF是矩形.
∵FD=FE,
∴矩形CEDF是正方形.
故(2)正确;
(3)∵△ADF≌△CEF,
∴S△ADF=S△CEF,
∴S四边形CEDF=S△AFC=$\frac{1}{2}$S△ABC.
故(3)错误;
(4)当FD垂直于AC时,三角形FDE的面积最小,而四边形CDFE的面积不变,此时三角形CDE的面积最大,而此时DE正好是最小值.所以C点到DF的距离最大,此时点C到线段DE的为$\frac{1}{2}$CF,即$\frac{1}{2}$×4×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$.
故(4)正确.
综上所述:(1)(2)(4)正确.
故选C.
点评 本题主要考查了等腰直角三角形的判定与性质、全等三角形的判定与性质、正方形的判定与性质、直角三角形斜边上的中线等于斜边的一半、勾股定理等知识,通过推理论证每个命题的正误是解决此类题目的关键.

 阅读快车系列答案
阅读快车系列答案
 如图,弦AC,BD相交于E,并且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,∠BEC=110°,则∠ACD的度数是75°.
如图,弦AC,BD相交于E,并且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,∠BEC=110°,则∠ACD的度数是75°.