题目内容
8. 如图,弦AC,BD相交于E,并且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,∠BEC=110°,则∠ACD的度数是75°.
如图,弦AC,BD相交于E,并且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,∠BEC=110°,则∠ACD的度数是75°.
分析 根据等弧对等角及等边对等角可得到∠BAC=∠BCA=∠CBD=∠CDB,再根据三角形外角的性质及三角形内角和定理求解即可.
解答 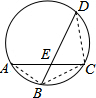 解:连接AB,BC,CD,
解:连接AB,BC,CD,
∵$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,
∴AB=BC=CD,
∴∠BAC=∠BCA=∠CBD=∠CDB,
∵∠BEC=110°
∴∠BCA=∠CBD=35°,∠CED=70°
∴∠ACD=180°-70°-35°=75°.
故答案为:75°.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.下列关于位似图形的表述:
①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;
④位似图形上任意两点与位似中心的距离之比等于位似比.
其中正确命题的序号是( )
①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;
④位似图形上任意两点与位似中心的距离之比等于位似比.
其中正确命题的序号是( )
| A. | ②③ | B. | ①② | C. | ③④ | D. | ②③④ |
13.下列代数式中,单项式共有( )
$\frac{3}{x}$,a-b,-2ab,$\frac{{x}^{2}+{y}^{2}}{5}$,0,$\frac{1}{2}$b2c3.
$\frac{3}{x}$,a-b,-2ab,$\frac{{x}^{2}+{y}^{2}}{5}$,0,$\frac{1}{2}$b2c3.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
17.若关于x,y的多项式$\frac{2}{5}{x^2}y-7mxy+\frac{3}{4}{y^3}+6xy$化简后不含二次项,则m=( )
| A. | $\frac{1}{7}$ | B. | $\frac{6}{7}$ | C. | $-\frac{6}{7}$ | D. | 0 |
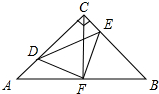 如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB=4,F是AB边上的中点,点D、E分别在AC、BC边上运动(点D不与点A,C重合),且始终保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,有下列结论:
如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB=4,F是AB边上的中点,点D、E分别在AC、BC边上运动(点D不与点A,C重合),且始终保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,有下列结论: