题目内容
10.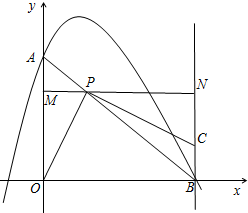 如图,抛物线y=-2x2+x+1交y轴于点A,交x轴正半轴于点B.P为线段AB上一动点,作直线PC⊥PO,交过点B垂直于x轴的直线于点C.过P点作直线MN平行于x轴,交y轴于点M,交过点B垂直于x轴的直线于点N.
如图,抛物线y=-2x2+x+1交y轴于点A,交x轴正半轴于点B.P为线段AB上一动点,作直线PC⊥PO,交过点B垂直于x轴的直线于点C.过P点作直线MN平行于x轴,交y轴于点M,交过点B垂直于x轴的直线于点N.(1)求点A,B的坐标;
(2)证明:OP=PC.
分析 (1)根据抛物线的解析式,易求得A、B的坐标;
(2)首先根据A、B的坐标,求出直线AB的解析式,设出点P的横坐标,利用直线AB的解析式,即可表示出P点的纵坐标,由此可得到MP、OM、PN的长,从而证得OM=PN,而∠OPC=90°,则∠OPM、∠PCN同为∠CPN的余角,再加上一组直角,即可由AAS判定△OPM≌△PCN,由此得证.
解答 解:(1)当x=0时,y=1,当y=0时,x=1或$x=-\frac{1}{2}$,
A(0,1),B(1,0);
(2)∵A(0,1),B(1,0),
∴直线AB:y=-x+1;
设P(a,-a+1),则有:
PM=a,OM=1-a,PN=MN-PM=1-a,
故OM=PN;
∵∠OPC=90°,则∠OPM+∠CPN=∠CPN+∠PCN=90°,
∴∠OPM=∠PCN;
在△OPM和△PCN中,
$\left\{\begin{array}{l}{∠OPM=∠PCN}\\{∠OMP=∠CPN=90°}\\{OM=PN}\end{array}\right.$
∴△OPM≌△PCN(AAS),
∴OP=CP.
点评 此题主要考查了抛物线与坐标轴交点坐标的求法、全等三角形的判定,利用数形结合的思想解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.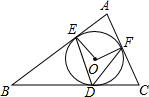 如图,⊙O内切于△ABC,切点分别为D,E,F,连接OE,OF,DE,DF,乙组∠A=80°,则∠EDF等于( )
如图,⊙O内切于△ABC,切点分别为D,E,F,连接OE,OF,DE,DF,乙组∠A=80°,则∠EDF等于( )
 如图,⊙O内切于△ABC,切点分别为D,E,F,连接OE,OF,DE,DF,乙组∠A=80°,则∠EDF等于( )
如图,⊙O内切于△ABC,切点分别为D,E,F,连接OE,OF,DE,DF,乙组∠A=80°,则∠EDF等于( )| A. | 40° | B. | 45° | C. | 50° | D. | 80° |
15.已知⊙O的直径AB=10cm,CD是⊙O的弦,CD⊥AB,垂足为M,且CD=8cm,则AC的长为( )
| A. | $2\sqrt{5}$ | B. | $2\sqrt{5}$或$4\sqrt{5}$ | C. | $4\sqrt{5}$ | D. | $2\sqrt{5}$或6 |
20.计算:$\sqrt{32}-\sqrt{8}$的结果是( )
| A. | $\sqrt{24}$ | B. | $2\sqrt{6}$ | C. | $3\sqrt{2}$ | D. | $2\sqrt{2}$ |
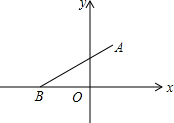 如图,在平面直角坐标系中,点A的坐标为(1,$\sqrt{3}$),点B在x轴的负半轴上,∠ABO=30°.
如图,在平面直角坐标系中,点A的坐标为(1,$\sqrt{3}$),点B在x轴的负半轴上,∠ABO=30°. 如图,4个小动物分别站在正方形场地的4个顶点,它们同时出发并以相同的速度沿场地边缘逆时针方向跑动,当它们同时停止时,顺次连接4个动物所在地点围成的图形是什么形状?为什么?
如图,4个小动物分别站在正方形场地的4个顶点,它们同时出发并以相同的速度沿场地边缘逆时针方向跑动,当它们同时停止时,顺次连接4个动物所在地点围成的图形是什么形状?为什么?