题目内容
15.已知⊙O的直径AB=10cm,CD是⊙O的弦,CD⊥AB,垂足为M,且CD=8cm,则AC的长为( )| A. | $2\sqrt{5}$ | B. | $2\sqrt{5}$或$4\sqrt{5}$ | C. | $4\sqrt{5}$ | D. | $2\sqrt{5}$或6 |
分析 先根据垂径定理得CM=DM=$\frac{1}{2}$CD=$\frac{1}{2}×8$=4,由直径AB=10cm,得OA=OC=5cm,由勾股定理得OM的长,利用勾股定理可得AC.
解答 解:∵CD⊥AB,
∴CM=DM=$\frac{1}{2}$CD=$\frac{1}{2}×8$=4,
∵AB=10,
∴OA=OC=5,
∴OM=$\sqrt{{OC}^{2}{-CM}^{2}}$=$\sqrt{{5}^{2}{-4}^{2}}$=3,
当如图1所示时,AM=AO+OM=8,
∴AC=$\sqrt{{AM}^{2}{+CM}^{2}}$=$\sqrt{{8}^{2}{+4}^{2}}$=4$\sqrt{5}$;
当如图2所示时,AM=AO-OM=2,
∴AC=$\sqrt{{AM}^{2}{+CM}^{2}}$=$\sqrt{{2}^{2}{+4}^{2}}$=2$\sqrt{5}$,
故选B.
点评 本题主要考查的是垂径定理,勾股定理及锐角三角函数的定义,熟知垂直于弦的直径平分弦,分类讨论是解答此题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
3.当x=-3时,$\sqrt{{x}^{2}}$的值是( )
| A. | ±3 | B. | 3 | C. | -3 | D. | 9 |
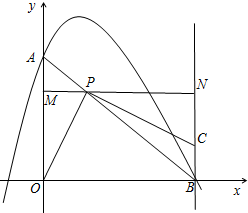 如图,抛物线y=-2x2+x+1交y轴于点A,交x轴正半轴于点B.P为线段AB上一动点,作直线PC⊥PO,交过点B垂直于x轴的直线于点C.过P点作直线MN平行于x轴,交y轴于点M,交过点B垂直于x轴的直线于点N.
如图,抛物线y=-2x2+x+1交y轴于点A,交x轴正半轴于点B.P为线段AB上一动点,作直线PC⊥PO,交过点B垂直于x轴的直线于点C.过P点作直线MN平行于x轴,交y轴于点M,交过点B垂直于x轴的直线于点N.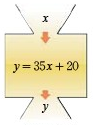 地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化,在某个地点y与x之间的关系可以近似地用关系式y=35x+20来表示.当x的值是5时,y=195.
地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化,在某个地点y与x之间的关系可以近似地用关系式y=35x+20来表示.当x的值是5时,y=195.