题目内容
20.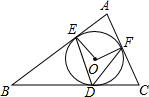 如图,⊙O内切于△ABC,切点分别为D,E,F,连接OE,OF,DE,DF,乙组∠A=80°,则∠EDF等于( )
如图,⊙O内切于△ABC,切点分别为D,E,F,连接OE,OF,DE,DF,乙组∠A=80°,则∠EDF等于( )| A. | 40° | B. | 45° | C. | 50° | D. | 80° |
分析 根据切线的性质得到∠OEA=∠OFA=90°,再利用四边形内角和可计算出∠EOF=180°-∠A=100°,然后根据圆周角定理可得到∠EDF的度数.
解答 解:∵⊙O内切于△ABC,
∴OE⊥AB,OF⊥AC,
∴∠OEA=∠OFA=90°,
∴∠EOF=180°-∠A=180°-80°=100°,
∴∠EDF=$\frac{1}{2}$∠EOF=50°.
故选C.
点评 本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心.三角形的内心就是三角形三个内角角平分线的交点.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
10.下列图形中,是正方体表面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
8.已知?ABCD中,若∠A+∠C=120°,则∠B的度数是( )
| A. | 100° | B. | 120° | C. | 80° | D. | 60° |
 某校学生骑自行车从学校去某地植树,过了一段时间学校派后勤人员开车去送树苗和植树工具,学生、后勤人员离开学校的距离y(千米)与行驶时间x(分钟)的函数图象如图所示.
某校学生骑自行车从学校去某地植树,过了一段时间学校派后勤人员开车去送树苗和植树工具,学生、后勤人员离开学校的距离y(千米)与行驶时间x(分钟)的函数图象如图所示. 如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中成立的有①②③.(只填序号)
如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中成立的有①②③.(只填序号) 如图,抛物线y=-2x2+x+1交y轴于点A,交x轴正半轴于点B.P为线段AB上一动点,作直线PC⊥PO,交过点B垂直于x轴的直线于点C.过P点作直线MN平行于x轴,交y轴于点M,交过点B垂直于x轴的直线于点N.
如图,抛物线y=-2x2+x+1交y轴于点A,交x轴正半轴于点B.P为线段AB上一动点,作直线PC⊥PO,交过点B垂直于x轴的直线于点C.过P点作直线MN平行于x轴,交y轴于点M,交过点B垂直于x轴的直线于点N.