题目内容
13. 如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).(1)求m及k的值;
如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).(1)求m及k的值;(2)求点C的坐标,并结合图象写出不等式组0<x+m≤$\frac{k}{x}$的解集.
(3)若A点关于直线y=x的对称点为A′,求△A′BC的面积.
分析 (1)把A的坐标代入两函数解析式,即可得出答案;
(2)求出一次函数的解析式,即可求出C的坐标,根据A、C的坐标,结合图象得出答案即可;
(3)根据对称和A的坐标求出A′的坐标,求出BW和A′C的值,根据面积公式得出即可.
解答 解:(1)把A的坐标代入y=x+m得:1=2+m,
解得:m=-1,
把A的坐标代入y=$\frac{k}{x}$得:1=$\frac{k}{2}$,
解得:k=2,
即m=-1,k=2;
(2)由(1)知:一次函数的解析式为y=x-1,反比例函数的解析式为y=$\frac{2}{x}$,
在y=x-1中,当y=0时,x=1,
即C的坐标为(1,0),
∵A(2,1),
∴不等式组0<x+m≤$\frac{k}{x}$的解集是1<x≤2;
(3)解方程组$\left\{\begin{array}{l}{y=\frac{2}{x}}\\{y=x-1}\end{array}\right.$得:$\left\{\begin{array}{l}{{x}_{1}=2}\\{{y}_{1}=1}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-1}\\{{y}_{2}=-2}\end{array}\right.$,
∵A(2,1)
∴B的坐标为(-1,-2),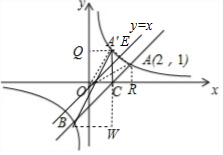
过A作AR⊥x轴于R,过A′作A′Q⊥y轴于Q,则∠A′QO=∠ARO=90°,
过B作BW⊥A′C于W,连接AA′,OA′,OA,
∵A、A′关于y=x对称,
∴OA′=OA,直线y=x垂直平分AA′,
∴∠A′OE=∠AOE,
∵直线y=x,
∴∠QOE=∠ROE,
∴∠QOA′=∠ROA,
在△A′QO和△ARO中
$\left\{\begin{array}{l}{∠A′QO=∠ARO}\\{∠QOA′=∠ROA}\\{OA′=OA}\end{array}\right.$
∴△A′QO≌△ARO(AAS),
∴△A′QO≌△ARO(AAS),
∴OQ=OR,A′Q=AR,
∵A(2,1),
∴A′Q=1,OQ=2,
∴A′的坐标为(1,2),
∵C(1,0),
∴A′C⊥x轴,
∵B(-1,-2),A′(1,2),
∴A′C=2,BW=1+1=2,
∴△A′BC的面积是$\frac{1}{2}×2×2$=2.
点评 本题考查了用待定系数法求一次函数和反比例函数的解析式,一次函数和反比例函数的交点问题,轴对称的性质等知识点,能够求出函数的解析式和A′的坐标是解此题的关键,注意数形结合思想的运用.

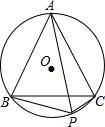 如图,等边△ABC是⊙O的内接三角形,P是$\widehat{BC}$上一点,当PB=3PC时,则△ABC与四边形ABPC的面积比为( )
如图,等边△ABC是⊙O的内接三角形,P是$\widehat{BC}$上一点,当PB=3PC时,则△ABC与四边形ABPC的面积比为( )| A. | $\frac{13}{16}$ | B. | $\frac{10}{13}$ | C. | $\frac{9}{11}$ | D. | $\frac{7}{9}$ |
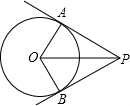 如图,PA,PB是⊙O的两条切线,切点分别是A,B,如果OP=4,PA=2$\sqrt{3}$,那么∠APB等于( )
如图,PA,PB是⊙O的两条切线,切点分别是A,B,如果OP=4,PA=2$\sqrt{3}$,那么∠APB等于( )| A. | 90° | B. | 100° | C. | 110° | D. | 60° |
| A. | 有两边及一角对应相等的两个三角形全等 | |
| B. | 面积之比为1:4的两个相似三角形的周长之比是1:2 | |
| C. | 方程x2-x-2=0有两个不相等的实数根 | |
| D. | 顺次连接任意四边形各边中点得到的四边形是平行四边形 |
| A. | x2+2x+4=0 | B. | x2+4x+2=0 | C. | x2+x-1=0 | D. | x2-3x=0 |
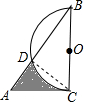 如图,在Rt△ABC中,∠B=30°,BC=$\sqrt{3}$,以BC为直径画半圆,交斜边AB于D,则图中阴影部分的面积为$\frac{5\sqrt{3}}{16}$-$\frac{π}{8}$.
如图,在Rt△ABC中,∠B=30°,BC=$\sqrt{3}$,以BC为直径画半圆,交斜边AB于D,则图中阴影部分的面积为$\frac{5\sqrt{3}}{16}$-$\frac{π}{8}$. 在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论:
在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论: 如图,是由5个相同的正方体组成的立体图形,从上面观察这个立体图形,得到的平面图形是( )
如图,是由5个相同的正方体组成的立体图形,从上面观察这个立体图形,得到的平面图形是( )


