题目内容
3.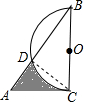 如图,在Rt△ABC中,∠B=30°,BC=$\sqrt{3}$,以BC为直径画半圆,交斜边AB于D,则图中阴影部分的面积为$\frac{5\sqrt{3}}{16}$-$\frac{π}{8}$.
如图,在Rt△ABC中,∠B=30°,BC=$\sqrt{3}$,以BC为直径画半圆,交斜边AB于D,则图中阴影部分的面积为$\frac{5\sqrt{3}}{16}$-$\frac{π}{8}$.
分析 连接OD,过O作OH⊥BD于H,由BC为直径,得到∠BDC=90°,解直角三角形得到BD=$\frac{3}{2}$,AC=$\frac{\sqrt{3}}{3}$BC=1,OH=$\frac{1}{2}$OB=$\frac{\sqrt{3}}{4}$,根据图形的面积公式即可得到结论.
解答  解:连接OD,过O作OH⊥BD于H,
解:连接OD,过O作OH⊥BD于H,
∵BC为直径,
∴∠BDC=90°,
∵∠B=30°,BC=$\sqrt{3}$,
∴∠DOC=60°,BD=$\frac{3}{2}$,
∵∠ACB=90°,
∴AC=$\frac{\sqrt{3}}{3}$BC=1,
∵∠OHB=90°,
∴OH=$\frac{1}{2}$OB=$\frac{\sqrt{3}}{4}$,
∴阴影部分的面积=S△ACB-S△BDC-S扇形ODC=$\frac{1}{2}×$1×$\sqrt{3}$-$\frac{1}{2}$×$\frac{3}{2}$×$\frac{\sqrt{3}}{4}$-$\frac{60π•(\frac{\sqrt{3}}{2})^{2}}{360}$=$\frac{5\sqrt{3}}{16}$-$\frac{π}{8}$,
故答案为:$\frac{5\sqrt{3}}{16}$-$\frac{π}{8}$.
点评 本题考查扇形面积公式、直角三角形30度角性质、解题的关键是学会分割法求面积,属于中考常考题型.

练习册系列答案
相关题目
13.下列实数中,是无理数的为( )
| A. | -3.567 | B. | 0.101001 | C. | $\sqrt{2}$ | D. | $\frac{1}{3}$ |
15.计算正确的是( )
| A. | (a+b)2=a2+b2 | B. | x2+x3=x5 | C. | (ab2)3=a2b5 | D. | 2a2•a-1=2a |
12.分式$\frac{a+b}{2ab}$(a,b均为正数),将字母的值都扩大为原来的2倍,则分式的值( )
| A. | 扩大为原来的2倍 | B. | 缩小为原来的$\frac{1}{2}$ | C. | 扩大为原来的4倍 | D. | 缩小为原来的$\frac{1}{4}$ |
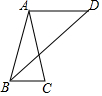 如图,已知AB=AC=AD,且∠C=2∠D,求证AD∥BC.
如图,已知AB=AC=AD,且∠C=2∠D,求证AD∥BC.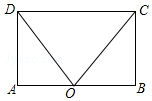 (1)已知x1=3是关于x的一元二次方程x2-4x+c=0的一个根,求c的值和方程的另一个根.
(1)已知x1=3是关于x的一元二次方程x2-4x+c=0的一个根,求c的值和方程的另一个根.
 如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).(1)求m及k的值;
如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).(1)求m及k的值;