题目内容
4.计算:(1)2$\sqrt{12}$-6$\sqrt{\frac{1}{3}}$+3$\sqrt{48}$
(2)($\frac{3}{2}$$\sqrt{1\frac{2}{3}}$-$\sqrt{1\frac{1}{4}}$)2.
分析 (1)先化简,再合并同类项即可求解;
(2)根据完全平方公式计算即可求解.)
解答 解:(1)2$\sqrt{12}$-6$\sqrt{\frac{1}{3}}$+3$\sqrt{48}$
=4$\sqrt{3}$-2$\sqrt{3}$+12$\sqrt{3}$
=14$\sqrt{3}$;
(2)($\frac{3}{2}$$\sqrt{1\frac{2}{3}}$-$\sqrt{1\frac{1}{4}}$)2
=$\frac{15}{4}$-2×$\frac{3}{2}$$\sqrt{1\frac{2}{3}×1\frac{1}{4}}$+$\frac{5}{4}$
=$\frac{15}{4}$-$\frac{5\sqrt{3}}{2}$+$\frac{5}{4}$
=5-$\frac{5\sqrt{3}}{2}$.
点评 此题考查了二次根式的混合运算,完全平方公式,关键是熟练掌握计算法则正确进行计算.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
15.计算正确的是( )
| A. | (a+b)2=a2+b2 | B. | x2+x3=x5 | C. | (ab2)3=a2b5 | D. | 2a2•a-1=2a |
12.分式$\frac{a+b}{2ab}$(a,b均为正数),将字母的值都扩大为原来的2倍,则分式的值( )
| A. | 扩大为原来的2倍 | B. | 缩小为原来的$\frac{1}{2}$ | C. | 扩大为原来的4倍 | D. | 缩小为原来的$\frac{1}{4}$ |
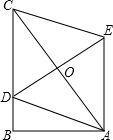 如图,在Rt△ABC中,∠B=90°,AB=3,∠BCA=30°,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE最小值是3.
如图,在Rt△ABC中,∠B=90°,AB=3,∠BCA=30°,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE最小值是3.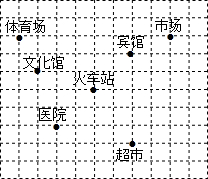 如图,已知火车站的坐标为(2,1),文化宫的坐标为(-1,2).
如图,已知火车站的坐标为(2,1),文化宫的坐标为(-1,2). 如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).(1)求m及k的值;
如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).(1)求m及k的值;