题目内容
2．下列命题为假命题的是（ ）| A． | 有两边及一角对应相等的两个三角形全等 | |
| B． | 面积之比为1：4的两个相似三角形的周长之比是1：2 | |
| C． | 方程x2-x-2=0有两个不相等的实数根 | |
| D． | 顺次连接任意四边形各边中点得到的四边形是平行四边形 |
分析 利用全等三角形的判定、相似三角形的性质、一元二次方程的根的判别式及中点四边形的知识分别判断后即可确定正确的结论．
解答 解：A、有两边及夹角对应相等的两个三角形全等，故错误，是假命题；
B、面积之比为1：4的两个相似三角形的周长之比是1：2，正确，是真命题；
C、方程x2-x-2=0有两个不相等的实数根，正确，是真命题；
D、顺次连接任意四边形各边中点得到的四边形是平行四边形，正确，是真命题，
故选A．
点评 本题考查了命题与定理的知识，解题的关键是了解全等三角形的判定、相似三角形的性质、一元二次方程的根的判别式及中点四边形的知识，难度不大．
练习册系列答案
相关题目
12．分式$\frac{a+b}{2ab}$（a，b均为正数），将字母的值都扩大为原来的2倍，则分式的值（ ）
| A． | 扩大为原来的2倍 | B． | 缩小为原来的$\frac{1}{2}$ | C． | 扩大为原来的4倍 | D． | 缩小为原来的$\frac{1}{4}$ |
如图，一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A，B两点，且与x轴交于点C，点A的坐标为（2，1）．（1）求m及k的值；
10．
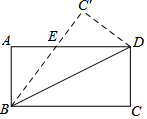如图，在矩形ABCD中，BC=6，CD=3，将△BCD沿对角线BD翻折，点C落在点C'处，BC'交AD于点E，则线段AE的长为（ ）
如图，在矩形ABCD中，BC=6，CD=3，将△BCD沿对角线BD翻折，点C落在点C'处，BC'交AD于点E，则线段AE的长为（ ）| A． | $\frac{9}{4}$ | B． | 3 | C． | $\frac{15}{4}$ | D． | $\frac{15}{2}$ |
17．计算$\sqrt{2}$•tan 60°的值等于（ ）
| A． | $\frac{\sqrt{5}}{3}$ | B． | $\frac{\sqrt{6}}{3}$ | C． | $\sqrt{5}$ | D． | $\sqrt{6}$ |
7．随着行政区划调整，2017年我区计划新建续建主次干道项目25个，全年计划完成交通投资19.79亿元，其中19.79亿元用科学记数法可表示为（ ）
| A． | 1.979×107元 | B． | 1.979×108元 | C． | 1.979×109元 | D． | 1.979×1010元 |
如图是由4个大小相同的正方体组合而成的几何体，其左视图是（ ）
1．M国股民吉姆上周末买进某公司月股票1000股，每股27 元，下表为本周内每日该股的涨跌情况 （星期六、日股市休市） （单位：元）
（1）星期三收盘时，每股是多少元？
（2）本周内每股最高价多少元？最低价是多少元？
（3）已知吉姆买进股票时付了1.5%的手续费，卖出时还需付成交额1.5%的手续费和1%的交易税，如果吉姆在星期五收盘前将全部股票卖出，他的收益情况如何？
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +6 | +6.5 | -1 | -2.5 | -6 |
（2）本周内每股最高价多少元？最低价是多少元？
（3）已知吉姆买进股票时付了1.5%的手续费，卖出时还需付成交额1.5%的手续费和1%的交易税，如果吉姆在星期五收盘前将全部股票卖出，他的收益情况如何？