题目内容
2. 如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.
如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.(1)求证:四边形ADCE是菱形;
(2)若AB=10,tan∠BAC=$\frac{1}{2}$,求菱形ADCE的面积.
分析 (1)根据DE∥BC,EC∥AB,得出EC∥DB且EC=DB,在Rt△ABC中,根据CD是边AB上的中线,得出四边形ADCE是平行四边形,求出∠AOD=∠ACB=90°,从而得出四边形ADCE是菱形;
(2)在Rt△ABC中,根据tan∠BAC=$\frac{BC}{AC}$=$\frac{1}{2}$,设BC=x,得出AC=2BC=2x,再根据勾股定理求出x的值,因为四边形DBCE是平行四边形,求出DE=BC=2$\sqrt{5}$,最后根据SADCE=$\frac{1}{2}$×AC×DE,代值计算即可.
解答 解:(1)∵DE∥BC,EC∥AB,
∴四边形DBCE是平行四边形,
∴EC∥DB,且EC=DB,
在Rt△ABC中,CD是边AB上的中线,
∴AD=DB=CD,
∴EC=AD,
∴四边形ADCE是平行四边形,
∴ED∥BC,
∴∠AOD=∠ACB,
∴∠ACB=90°,
∴∠AOD=∠ACB=90°,
∴四边形ADCE是菱形;
(2)在Rt△ABC中,tan∠BAC=$\frac{BC}{AC}$=$\frac{1}{2}$,
设BC=x,
∴AC=2BC=2x,
由勾股定理得:x2+(2x)2=102,
解得:x=2$\sqrt{5}$,
∵四边形DBCE是平行四边形,
∴DE=BC=2$\sqrt{5}$,
∴SADCE=$\frac{1}{2}$×AC×DE=$\frac{1}{2}$×4$\sqrt{5}$×2$\sqrt{5}$=20.
点评 此题主要考查了菱形的性质和判定以及面积的计算,使学生能够灵活运用菱形知识解决有关问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.将一块a×b×c(a<b<c)的长方体铁块(图1)放入一个长方体水槽(图2),铁块与水槽的四壁不接触,现向水槽内匀速注水,直至注满水槽为止,因铁块在水槽内有3种不同的放置方式,所以水槽内的水深h与注水时间t的函数关系用图象来反映,其全过程有三种不同的图象(图3,图4,图5)(注:长度单位:厘米;时间单位:秒),则下列结论中,不正确的是( )
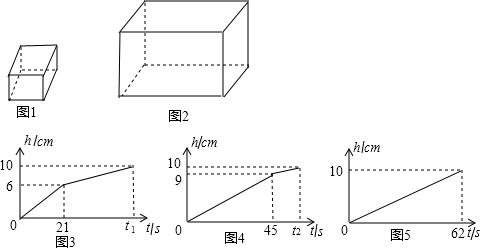

| A. | 水槽的深度是10cm | B. | a+b=15 | ||
| C. | 铁块的体积是150cm3 | D. | t1=t2 |
10.若a<0,则点M(-a,a)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7. 如图,在圆内接四边形ABCD中,∠B=50°,则∠D=( )
如图,在圆内接四边形ABCD中,∠B=50°,则∠D=( )
 如图,在圆内接四边形ABCD中,∠B=50°,则∠D=( )
如图,在圆内接四边形ABCD中,∠B=50°,则∠D=( )| A. | 40° | B. | 130° | C. | 120° | D. | 150° |
 如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,找出图中相等的角,并说明理由.
如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,找出图中相等的角,并说明理由.