题目内容
在等边△ABC中,边AB=2cm,点D是边BC的中点,点E是从点B沿B→A→C的方向开始运动的一个动点,速度为1cm/s,当E点运动t秒时,

(1)当△BED是直角三角形时,求t的值;
(2)当DE将△ABC的周长分成的两部分之间是2倍的关系时,求t的值;
(3)当点E只在边AC上运动时,是否存在一点E使得DE+BE的值取得最小值?如果不存在,请说明理由;如果存在,请直接写出此时DE+BE的最小值(不要求写过程).

(1)当△BED是直角三角形时,求t的值;
(2)当DE将△ABC的周长分成的两部分之间是2倍的关系时,求t的值;
(3)当点E只在边AC上运动时,是否存在一点E使得DE+BE的值取得最小值?如果不存在,请说明理由;如果存在,请直接写出此时DE+BE的最小值(不要求写过程).
考点:轴对称-最短路线问题,一元一次方程的应用,含30度角的直角三角形
专题:分类讨论
分析:(1)分两种情况讨论即可求得;
(2)由于动点E从B点出发,沿B→A→C的方向运动,所以分两种情况进行讨论:(1)E点在AB上,设运动时间为t,用含t的代数式分别表示BE,AE,根据条件过D、E两点的直线将△ABC的周长分成两个部分,使其中一部分是另一部分的2倍,求出t值;(2)E点在AC上,同理,可解出t的值.
(3)作B关于AC的对称点B′,然后连接BD交AC于E,即为所求;此时DE+BE=B′D,作BG⊥BC于G,根据30°的直角三角形的性质求得B′G=
,BG=3,进而求得DG,根据勾股定理即可求得.
(2)由于动点E从B点出发,沿B→A→C的方向运动,所以分两种情况进行讨论:(1)E点在AB上,设运动时间为t,用含t的代数式分别表示BE,AE,根据条件过D、E两点的直线将△ABC的周长分成两个部分,使其中一部分是另一部分的2倍,求出t值;(2)E点在AC上,同理,可解出t的值.
(3)作B关于AC的对称点B′,然后连接BD交AC于E,即为所求;此时DE+BE=B′D,作BG⊥BC于G,根据30°的直角三角形的性质求得B′G=
| 3 |
解答:解:(1)分两种情况:
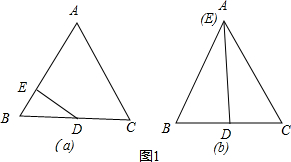
当∠BED=90°时,
如图1,∵△ABC是等边三角形,
∴∠B=60°,
∴∠BDE=30°,
∴BE=
BD,
∵AB=AC=BC=2cm,BD=CD=
BC=
×2=1cm,
∴BE=
cm,
∴t=
秒;
当∠BDE=90°时,
∵△ABC是等边三角形,BD=DC,
∴E与A重合,
∴BE=AB=2cm.
∴t=2秒
(2)分两种情况:
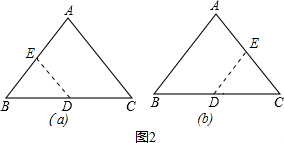
E点在AB上时,如图,
∵AB=AC=2cm,BD=CD=
BC=
×2=1cm,
设E点运动了t秒,则BE=t,AE=2-t,由题意得:
BE+BD=
(AE+AC+CD),
∴t+1=
(2-t+2+1),
解得t=1秒;
E点在AC上时,如图,
∵AB=AC=BC=2cm,BD=CD=
BC=
×2=1cm,E点运动了t秒,
则AB+AE=t,EC=AB+AC-t=4-t,
由题意得:BD+AB+AE=2(EC+CD),
∴1+t=2(4-t+1),
解得t=3秒.
故当t=1或3秒时,DE把△ABC的周长分成的两部分之间是2倍的关系.
(3)作B关于AC的对称点B′,然后连接BD交AC于E,即为所求;此时DE+BE=B′D;
作BG⊥BC于G,
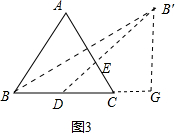
∴△ABC是等边三角形,BC=2,
∴∠B′BC=30°,B′B=2
,
∴B′G=
,BG=3,
∵BD=CD=1,
∴DG=2,
在RT△B′GD中,B′D=
=
.
∴DE+BE的最小值=
.

当∠BED=90°时,
如图1,∵△ABC是等边三角形,
∴∠B=60°,
∴∠BDE=30°,
∴BE=
| 1 |
| 2 |
∵AB=AC=BC=2cm,BD=CD=
| 1 |
| 2 |
| 1 |
| 2 |
∴BE=
| 1 |
| 2 |
∴t=
| 1 |
| 2 |
当∠BDE=90°时,
∵△ABC是等边三角形,BD=DC,
∴E与A重合,
∴BE=AB=2cm.
∴t=2秒
(2)分两种情况:

E点在AB上时,如图,
∵AB=AC=2cm,BD=CD=
| 1 |
| 2 |
| 1 |
| 2 |
设E点运动了t秒,则BE=t,AE=2-t,由题意得:
BE+BD=
| 1 |
| 2 |
∴t+1=
| 1 |
| 2 |
解得t=1秒;
E点在AC上时,如图,
∵AB=AC=BC=2cm,BD=CD=
| 1 |
| 2 |
| 1 |
| 2 |
则AB+AE=t,EC=AB+AC-t=4-t,
由题意得:BD+AB+AE=2(EC+CD),
∴1+t=2(4-t+1),
解得t=3秒.
故当t=1或3秒时,DE把△ABC的周长分成的两部分之间是2倍的关系.
(3)作B关于AC的对称点B′,然后连接BD交AC于E,即为所求;此时DE+BE=B′D;
作BG⊥BC于G,

∴△ABC是等边三角形,BC=2,
∴∠B′BC=30°,B′B=2
| 3 |
∴B′G=
| 3 |
∵BD=CD=1,
∴DG=2,
在RT△B′GD中,B′D=
| DG2+B′G2 |
| 7 |
∴DE+BE的最小值=
| 7 |
点评:此题考查等边三角形的性质,含30°的直角三角形的性质,轴对称-最短路线问题,还涉及到了动点,对于初二学生来说是个难点,解答此题时要分两种情况讨论,不要漏解.

练习册系列答案
相关题目
如图,将半径为2、圆心角为60°的扇形纸片AOB,在直线l上向右作无滑动的滚动至扇形A′O′B′处,则顶点O经过的路线总长为( )


| A、3π | ||
| B、4π | ||
C、
| ||
D、
|
有下列命题:①两点之间,线段最短; ②相等的角是对顶角; ③当a>0时,|a|=a; ④内错角互补,两直线平行.其中真命题的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
下列四个命题中真命题是( )
| A、三点确定一个圆 |
| B、对角线互相垂直且相等的四边形是正方形 |
| C、若Rt△ABC中,∠C=90°,则sinA=cosB |
| D、三角形的内心到三角形三个顶点的距离相等 |
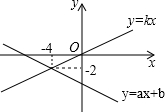 如图,已知一次函数y=ax+b(a≠0)和y=kx(k≠0)的图象交于点P,则一元一次不等式ax+b≤kx的解集是
如图,已知一次函数y=ax+b(a≠0)和y=kx(k≠0)的图象交于点P,则一元一次不等式ax+b≤kx的解集是