��Ŀ����
3�� ��ͼ����?ABCD�У�AB��AC��AB=1��BC=$\sqrt{5}$���Խ���BD��AC���ڵ�O����ֱ��AC�Ƶ�O˳ʱ����ת�ֱ�BC��AD�ڵ�E��F��
��ͼ����?ABCD�У�AB��AC��AB=1��BC=$\sqrt{5}$���Խ���BD��AC���ڵ�O����ֱ��AC�Ƶ�O˳ʱ����ת�ֱ�BC��AD�ڵ�E��F����1����˵������ת�����У�AF��CE�ܱ�����ȣ�
��2������ת��Ϊ90��ʱ���ж��ı���ABEF����״��֤����
��3������ת�����У��ı���BEDF������������������ܣ���˵�����ɣ�����ܣ������ʱAC �Ƶ�O˳ʱ����ת�ĽǶȣ�
���� ��1������ƽ���ı��ε����ʵó�AD��BC��OA=OC�������1=��2������ASA�Ƴ���AOF�ա�COE���ɣ�
��2�����BA��EF������ƽ���ı��ε����ʵó�AD��BC����AF��BE������ƽ���ı��ε��ж��ó����ɣ�
��3������ı���BEDF��ƽ���ı��Σ��������ε��ж��ó����ɣ������AOB�����������3�����ɵó��𰸣�
��� �⣺��1�����ڡ�ABCD�У�AD��BC��OA=OC��
���1=��2��
�ڡ�AOF�͡�COEE�У�
$\left\{\begin{array}{l}{��1=��2}\\{OA=OC}\\{��3=��4}\end{array}\right.$
���AOF�ա�COE��ASA����
��AF=CE��
��2���ı���ABEF��ƽ���ı��Σ�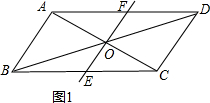
�����⣬��AOF=90�㣬����ͼ1����
�֡�AB��AC��
���BAO=90�㣬��AOF=90�㣬
���BAO=��AOF��
��BA��EF��
���ı���ABCD��ƽ���ı��Σ�
��AD��BC����AF��BE��
��BA��EF��AF��BE��
���ı���ABEF��ƽ���ı��Σ�
��3����EF��BDʱ���ı���BEDF�����Σ���ͼ2����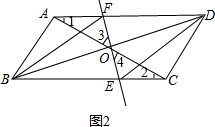
��AF=CE��AD��BC��AD=BC��
��FD��BE��DF=BE��
���ı���BEDF��ƽ���ı��Σ�
�֡�EF��BD��
���BEDF������
��AB��AC��
���BAC=90�㣬
��BC2=AB2+AC2��
��AB=1��BC=$\sqrt{5}$��
��AC=$\sqrt{B{C^2}+A{B^2}}$=2��
���ı���ABCD��ƽ���ı��Σ�
��OA=$\frac{1}{2}$AC=$\frac{1}{2}$��2=1��
���ڡ�AOB�У�AB=AO=1����BAO=90�㣬
���AOB=��ABO=45�㣬
��EF��BD��
���BOF=90�㣬
���3=��BOF-��AOB=90��-45��=45�㣬
����ת��Ϊ45�㣮
���� ���⿼����ƽ���ı��ε����ʺ��ж������ε����ʺ��ж�����ת�����ʣ����ɶ�����Ӧ�ã����ۺ�����֪ʶ����������ǽ����Ĺؼ���

 ����ʦ���һ��һ��ϵ�д�
����ʦ���һ��һ��ϵ�д�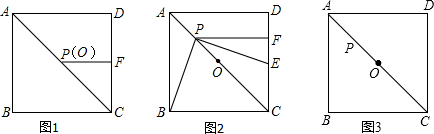
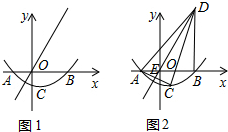
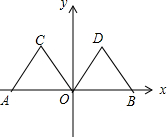 ��ͼ����ƽ��ֱ������ϵ�У���A������Ϊ��-2��0�����ȱߡ�AOC����ƽ�ƻ���Գƻ���ת�����Եõ���OBD��
��ͼ����ƽ��ֱ������ϵ�У���A������Ϊ��-2��0�����ȱߡ�AOC����ƽ�ƻ���Գƻ���ת�����Եõ���OBD��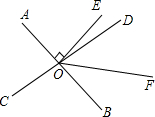 ��ͼ��ֱ��AB��CD�ཻ�ڵ�O��OE��AB����AOC����AOD=4��5��OFƽ�֡�BOD�����EOF�Ķ�����
��ͼ��ֱ��AB��CD�ཻ�ڵ�O��OE��AB����AOC����AOD=4��5��OFƽ�֡�BOD�����EOF�Ķ����� ��ͼ����?ABCD�У�AE�sEB=1�s2��
��ͼ����?ABCD�У�AE�sEB=1�s2�� ��ͼ����P������ABCD�ĶԽ���BD��һ�㣬����CP���ӳ�����AD��E����BA���ӳ����ڵ�F��
��ͼ����P������ABCD�ĶԽ���BD��һ�㣬����CP���ӳ�����AD��E����BA���ӳ����ڵ�F��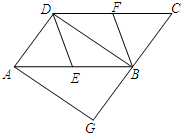 ��ͼ����?ABCD�У�E��F�ֱ�Ϊ��AB��CD���е㣬BD�ǶԽ��ߣ�����A��AG��DB����CB���ӳ����ڵ�G����G=90�㣮
��ͼ����?ABCD�У�E��F�ֱ�Ϊ��AB��CD���е㣬BD�ǶԽ��ߣ�����A��AG��DB����CB���ӳ����ڵ�G����G=90�㣮