��Ŀ����
1��������ABCD�У���O�ǶԽ���AC���е㣬P�ǶԽ���AC��һ���㣬����P��PF��CD�ڵ�F����ͼ1������P���O�غ�ʱ����Ȼ��DF=CF��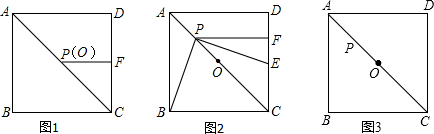
��1����ͼ2������P���߶�AO�ϣ������A��O�غϣ���PE��PB��PE��CD�ڵ�E��
����֤��DF=EF��
��д���߶�PC��PA��CE֮���һ��������ϵ����֤����Ľ��ۣ�
��2������P���߶�OC�ϣ������O��C�غϣ���PE��PB��PE��ֱ��CD�ڵ�E�������ͼ3���жϣ�1���еĽ��ۢ١����Ƿ�ֱ����������������д����Ӧ�Ľ��ۣ�����д���۾�����֤����
���� ��1���������ε�����֤�á�BQP�ա�PFE���Ӷ��õ�DF=EF�����ڡ�PCF�͡�PAG��Ϊ����ֱ�������Σ�����PA=$\sqrt{2}$PG��PC=$\sqrt{2}$CF����PA=$\sqrt{2}$EF�������õ�PC��PA��CE�����ϵΪ��PC=$\sqrt{2}$CE+PA��
��2��ͬ��1��֤��DF=EF�������߶ε�������ϵ��PA-PC=$\sqrt{2}$CE��
��� �⣺
��1����ͼ2���ӳ�FP��AB�ڵ�Q��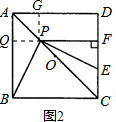
�١�AC��������ABCD�Խ��ߣ�
���QAP=��APQ=45�㣬
��AQ=PQ��
��AB=QF��
��BQ=PF��
��PE��PB��
���QPB+��FPE=90�㣬
�ߡ�QBP+��QPB=90�㣬
���QBP=��FPE��
�ߡ�BQP=��PFE=90�㣬
���BQP�ա�PFE��
��QP=EF��
��AQ=DF��
��DF=EF��
����ͼ2������P��PG��AD��
��PF��CD����PCF=��PAG=45�㣬
���PCF�͡�PAG��Ϊ����ֱ�������Σ�
���ı���DFPGΪ���Σ�
��PA=$\sqrt{2}$PG��PC=$\sqrt{2}$CF��
��PG=DF��DF=EF��
��PA=$\sqrt{2}$EF��
��PC=$\sqrt{2}$CF=$\sqrt{2}$��CE+EF��=$\sqrt{2}$CE+$\sqrt{2}$EF=$\sqrt{2}$CE+PA��
��PC��PA��CE�����ϵΪ��PC=$\sqrt{2}$CE+PA��
��2�����ۢ��Գ��������ۢڲ���������ʱ���������߶ε�������ϵ��PA-PC=$\sqrt{2}$CE��
��ͼ3��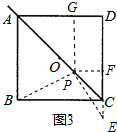
�١�PB��PE��BC��CE��
��B��P��C��E�ĵ㹲Բ��
���PEC=��PBC��
�ڡ�PBC�͡�PDC���У�BC=DC����֪������PCB=��PCD=45�㣨��֤����PC�߹����ߣ�
���PBC�ա�PDC��SAS����
���PBC=��PDC��
���PEC=��PDC��
��PF��DE��
��DF=EF��
��ͬ����PA=$\sqrt{2}$PG=$\sqrt{2}$DF=$\sqrt{2}$EF��PC=$\sqrt{2}$CF��
��PA=$\sqrt{2}$EF=$\sqrt{2}$��CE+CF��=$\sqrt{2}$CE+$\sqrt{2}$CF=$\sqrt{2}$CE+PC
��PC��PA��CE�����ϵΪ��PA-PC=$\sqrt{2}$CE��
���� ������һ����̬�����⣬���������������ʡ��߶δ�ֱƽ���ߵ����ʡ����������Ƶ����������ʽ�����������˼���ͱ���������������������������ȫ���ǽ���Ĺؼ��������漰֪ʶ��϶࣬�ۺ��Ժ�ǿ���Ѷ����У�

 ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
ȫ�ŵ�����Ԫ�ƻ�ϵ�д� ��ͼ��ֱ��a��b��c�ཻ�ڵ�A��ֱ��c��d��e�ཻ�ڵ�B����ͼ�������ڴ��ǵ��ǣ�������
��ͼ��ֱ��a��b��c�ཻ�ڵ�A��ֱ��c��d��e�ཻ�ڵ�B����ͼ�������ڴ��ǵ��ǣ�������| A�� | ��1�͡�2 | B�� | ��2�͡�3 | C�� | ��1�͡�3 | D�� | ��3�͡�4 |
 ��ͼ��ֱ��AB��CD�ཻ�ڵ�O����AOD+��BOC=200�㣬���AOC�Ķ���Ϊ��������
��ͼ��ֱ��AB��CD�ཻ�ڵ�O����AOD+��BOC=200�㣬���AOC�Ķ���Ϊ��������| A�� | 120�� | B�� | 100�� | C�� | 90�� | D�� | 80�� |
 ��ͼ���ھ���ABCD�У�$\frac{AB}{BC}=\frac{3}{5}$��ACΪ�Խ��ߣ�BM��AC�ڵ�M����AD�ڵ�N����O��BC����һ�㣬$\frac{OC}{BC}=\frac{1}{3}$������DO��AC�ڵ�P��OF��OD��BN�ڵ�E����AB���ڵ�F��
��ͼ���ھ���ABCD�У�$\frac{AB}{BC}=\frac{3}{5}$��ACΪ�Խ��ߣ�BM��AC�ڵ�M����AD�ڵ�N����O��BC����һ�㣬$\frac{OC}{BC}=\frac{1}{3}$������DO��AC�ڵ�P��OF��OD��BN�ڵ�E����AB���ڵ�F��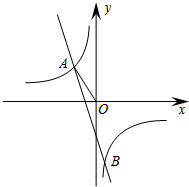 ��֪����������y=$\frac{k_1}{3x}$��ͼ����һ�κ���y=k2x+m��ͼ����A��a��1����B��$\frac{1}{3}$��-3�����㣬����AO��
��֪����������y=$\frac{k_1}{3x}$��ͼ����һ�κ���y=k2x+m��ͼ����A��a��1����B��$\frac{1}{3}$��-3�����㣬����AO��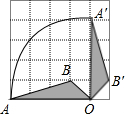 ��ͼ����5��5�������������У�ÿ��С�����εı߳���Ϊ1��������AOB�Ƶ�O˳ʱ����ת90��õ���A��OB�䣬��A���˶���·��$\widehat{AA��}$�ij�Ϊ��������
��ͼ����5��5�������������У�ÿ��С�����εı߳���Ϊ1��������AOB�Ƶ�O˳ʱ����ת90��õ���A��OB�䣬��A���˶���·��$\widehat{AA��}$�ij�Ϊ��������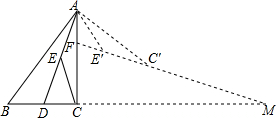 ��Rt��ABC�У���ACB=90�㣬BC=3��AC=4��ADƽ�֡�CAB��BC�ڵ�D��EΪAD���е㣬����CE������ACE�Ƶ�A��ʱ����ת����AE��C�䣬ֱ��E��C�佻AC�ڵ�F����BC���ӳ����ڵ�M����AF=E��F����CM=$\frac{96-10\sqrt{10}}{7}$��
��Rt��ABC�У���ACB=90�㣬BC=3��AC=4��ADƽ�֡�CAB��BC�ڵ�D��EΪAD���е㣬����CE������ACE�Ƶ�A��ʱ����ת����AE��C�䣬ֱ��E��C�佻AC�ڵ�F����BC���ӳ����ڵ�M����AF=E��F����CM=$\frac{96-10\sqrt{10}}{7}$�� ��ͼ����?ABCD�У�AB��AC��AB=1��BC=$\sqrt{5}$���Խ���BD��AC���ڵ�O����ֱ��AC�Ƶ�O˳ʱ����ת�ֱ�BC��AD�ڵ�E��F��
��ͼ����?ABCD�У�AB��AC��AB=1��BC=$\sqrt{5}$���Խ���BD��AC���ڵ�O����ֱ��AC�Ƶ�O˳ʱ����ת�ֱ�BC��AD�ڵ�E��F��