题目内容
在△ABC中,AB=AC=4,腰上高CH为2
.E是BC上一点,EF∥AB交AC于F,EP⊥AB垂足为P.设BP=x,梯形BEFA的面积为y.求:
(1)y与x的函数关系及定义域;
(2)当梯形BEFA面积为△ABC面积一半时,求BP的长.
| 3 |
(1)y与x的函数关系及定义域;
(2)当梯形BEFA面积为△ABC面积一半时,求BP的长.
考点:相似三角形的判定与性质,一元二次方程的应用,勾股定理
专题:
分析:(1)由条件可证明△ABC为等边三角形,再利用x表示出EF的长和PE的长可得到y与x的函数关系式;
(2)可先求得△ABC的面积,当y=
S△ABC,代入函数解析式求出x即可.
(2)可先求得△ABC的面积,当y=
| 1 |
| 2 |
解答: 解:(1)∵AC=4,CH=2
解:(1)∵AC=4,CH=2
,
∴sin∠A=
=
=
,
∴∠A=60°,且AB=AC,
∴△ABC为等边三角形,
∴∠B=60°,AB=BC=AC=4,
∵EF∥AB,
∴△CEF为等边三角形,
∴EF=CE,
当BP=x,则BE=2x,PE=
x,
∴EF=CE=BC-BE=4-2x,
∴y=
(AB+EF)•PE=
×(4+4-2x)×
x=-
x2+4
x,
∵P点在AB上,
∴0<x<4,
综上可知y与x的函数关系为y═-
x2+4x,其定义域为0<x<4;
(2)∵S△ABC=
AB•CH=
×4×2
=4
,
∴当梯形BEFA面积为△ABC面积一半时,y=2
,
∴2
=-
x2+4
x,解得x=2+
或x=2-
,
即当梯形BEFA面积为△ABC面积一半时,BP的长为2+
或2-
.
 解:(1)∵AC=4,CH=2
解:(1)∵AC=4,CH=2| 3 |
∴sin∠A=
| CH |
| AC |
2
| ||
| 4 |
| ||
| 2 |
∴∠A=60°,且AB=AC,
∴△ABC为等边三角形,
∴∠B=60°,AB=BC=AC=4,
∵EF∥AB,
∴△CEF为等边三角形,
∴EF=CE,
当BP=x,则BE=2x,PE=
| 3 |
∴EF=CE=BC-BE=4-2x,
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
∵P点在AB上,
∴0<x<4,
综上可知y与x的函数关系为y═-
| 3 |
(2)∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴当梯形BEFA面积为△ABC面积一半时,y=2
| 3 |
∴2
| 3 |
| 3 |
| 3 |
| 2 |
| 2 |
即当梯形BEFA面积为△ABC面积一半时,BP的长为2+
| 2 |
| 2 |
点评:本题主要考查等边三角形的判定和性质,由条件判定出△ABC为等边三角形是解题的关键.

练习册系列答案
相关题目
下列命题是真命题的是( )
| A、4是2的平方根 |
| B、2是4的算术平方根 |
| C、0的算术平方根不存在 |
| D、-1是-1的算术平方根 |
 如图,四边形ABCD,EFGH分别是⊙O的外切正四边形和内接正四边形,则
如图,四边形ABCD,EFGH分别是⊙O的外切正四边形和内接正四边形,则| EF |
| AB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 在△ABC中,∠ABC=90°,AC=BC,线段AD是△ABC的角平分线,过点B作AD的垂线交AD的延长线于点E,若BE=4,则AD=
在△ABC中,∠ABC=90°,AC=BC,线段AD是△ABC的角平分线,过点B作AD的垂线交AD的延长线于点E,若BE=4,则AD=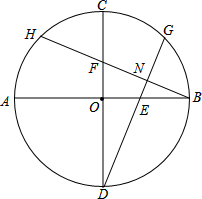 在⊙O中,已知直径AB与直径CD垂直于O,E在OB上,F在OC,且OE=OF,连接DE且延长交⊙O于G,连接BF且延长交⊙O于H,BH与DG相交于N.求证:BH⊥GD.
在⊙O中,已知直径AB与直径CD垂直于O,E在OB上,F在OC,且OE=OF,连接DE且延长交⊙O于G,连接BF且延长交⊙O于H,BH与DG相交于N.求证:BH⊥GD. 如图所示,AD是△ABC的角平分线,CE∥AD交BA的延长线于点E,求证:
如图所示,AD是△ABC的角平分线,CE∥AD交BA的延长线于点E,求证: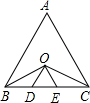 如图,在等边三角形ABC中,∠B、∠C的平分线交于O,过O作OD∥AB,OE∥AC,OD和OE分别交BC于点D、E.求证:BD=DE=EC.
如图,在等边三角形ABC中,∠B、∠C的平分线交于O,过O作OD∥AB,OE∥AC,OD和OE分别交BC于点D、E.求证:BD=DE=EC.