题目内容
 在△ABC中,∠ABC=90°,AC=BC,线段AD是△ABC的角平分线,过点B作AD的垂线交AD的延长线于点E,若BE=4,则AD=
在△ABC中,∠ABC=90°,AC=BC,线段AD是△ABC的角平分线,过点B作AD的垂线交AD的延长线于点E,若BE=4,则AD=考点:全等三角形的判定与性质
专题:
分析:延长AC,BE交于点F,易证∠EBD=∠DAC,即可证明△CBF≌△CAD,可得AD=BF,易证△ABF是等腰三角形,可得BE=EF,即可解题.
解答:解:延长AC,BE交于点F,
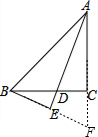
∵∠ADC+∠CAD=90°,∠EBD+∠BDE=90°,∠BDE=∠ADC,
∴∠EBD=∠DAC,
在△CBF和△CAD中,
,
∴△CBF≌△CAD(ASA),
∴AD=BF,
∵△ABF中,AE⊥BF,∠BAE=∠FAE,
∴△ABF是等腰三角形,
∴BE=EF,
∴AD=2BE=8.

∵∠ADC+∠CAD=90°,∠EBD+∠BDE=90°,∠BDE=∠ADC,
∴∠EBD=∠DAC,
在△CBF和△CAD中,
|
∴△CBF≌△CAD(ASA),
∴AD=BF,
∵△ABF中,AE⊥BF,∠BAE=∠FAE,
∴△ABF是等腰三角形,
∴BE=EF,
∴AD=2BE=8.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△CBF≌△CAD是解题的关键.

练习册系列答案
相关题目
在3.14,
,0,
,
,0.150250015…中,无理数有( )
| 13 |
| 3 | 8 |
| 3 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
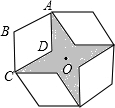 如图是将菱形ABCD以点O为中心分别旋转90°,180°,270°后形成的图形,若∠BAD=60°,AB=2,则图中的阴影部分的面积为( )
如图是将菱形ABCD以点O为中心分别旋转90°,180°,270°后形成的图形,若∠BAD=60°,AB=2,则图中的阴影部分的面积为( )| A、8 | ||
B、12-4
| ||
C、1+
| ||
D、12-2
|
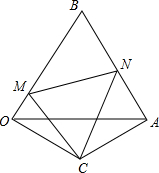 如图,△BOA是边长为2的等边三角形,OC=AC,∠OCA=120°,点M在OB边上,连接CM,将CM绕点C顺时针方向旋转60°,交AB于点N,连接MN,则△BMN的周长是
如图,△BOA是边长为2的等边三角形,OC=AC,∠OCA=120°,点M在OB边上,连接CM,将CM绕点C顺时针方向旋转60°,交AB于点N,连接MN,则△BMN的周长是
 如图,在△ABC中,AC=AB,∠BAC=90°,D是BC上的一动点,过点C作CE⊥BC,连接DE,求证:∠BAD=∠EDC.
如图,在△ABC中,AC=AB,∠BAC=90°,D是BC上的一动点,过点C作CE⊥BC,连接DE,求证:∠BAD=∠EDC. 如图,在△ABC中,AD平分∠BAC,DG⊥BC于点G,BG=CG,DE⊥AB于点E,DF⊥AC交AC的延长线于点F.求证:BE=CF.
如图,在△ABC中,AD平分∠BAC,DG⊥BC于点G,BG=CG,DE⊥AB于点E,DF⊥AC交AC的延长线于点F.求证:BE=CF.