题目内容
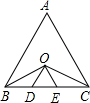 如图,在等边三角形ABC中,∠B、∠C的平分线交于O,过O作OD∥AB,OE∥AC,OD和OE分别交BC于点D、E.求证:BD=DE=EC.
如图,在等边三角形ABC中,∠B、∠C的平分线交于O,过O作OD∥AB,OE∥AC,OD和OE分别交BC于点D、E.求证:BD=DE=EC.考点:等边三角形的判定与性质
专题:
分析:由条件可证明∠OBD=∠BOD=30°,可得OD=BD,∠ODB=120°,同理可得OE=EC,∠OED=60°,从而求得△ODE是等边三角形,得出OD=OE=DE,即可求得结论.
解答:解:∵OD∥AB,BO平分∠ABC,
∴∠ABO=∠BOD=∠OBD=30°,
∴OD=BD,∠ODB=120°,
∴∠ODE=60°,
同理可得OE=EC,∠OED=60°,
∴△ODE是等边三角形,
∴OD=OE=DE,
∴BD=DE=EC.
∴∠ABO=∠BOD=∠OBD=30°,
∴OD=BD,∠ODB=120°,
∴∠ODE=60°,
同理可得OE=EC,∠OED=60°,
∴△ODE是等边三角形,
∴OD=OE=DE,
∴BD=DE=EC.
点评:本题主要考查等边三角形的性质及平行线的性质、角平分线的定义,由条件求得OD=BD、OE=EC,以及等边三角形ODE是解题的关键.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
下列命题是真命题的是( )
| A、相等的角是对顶角 |
| B、三角形中有两个角的和大于180°,则这个三角形是锐角三角形 |
| C、对角线相等的四边形是矩形 |
| D、垂直平分线上的点到线段两端点的距离相等 |
 如图,在△ABC中,AD平分∠BAC,DG⊥BC于点G,BG=CG,DE⊥AB于点E,DF⊥AC交AC的延长线于点F.求证:BE=CF.
如图,在△ABC中,AD平分∠BAC,DG⊥BC于点G,BG=CG,DE⊥AB于点E,DF⊥AC交AC的延长线于点F.求证:BE=CF. 如图,在四边形ABCD中,∠B=∠C=60°,点P在BC上,点E在DC上,且∠APE=∠B,
如图,在四边形ABCD中,∠B=∠C=60°,点P在BC上,点E在DC上,且∠APE=∠B,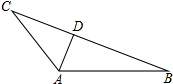 如图,
如图,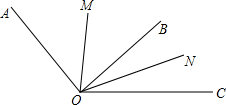 如图,设相邻两个角∠AOB,∠BOC的角平分线分别为OM,ON,如果∠MON=α(α为常数),那么∠AOC的度数是否为一个固定值?若是,请说明理由,并求出∠AOC的度数;若不是,请说明理由.
如图,设相邻两个角∠AOB,∠BOC的角平分线分别为OM,ON,如果∠MON=α(α为常数),那么∠AOC的度数是否为一个固定值?若是,请说明理由,并求出∠AOC的度数;若不是,请说明理由. 如图,△ABC中,∠A=70°,DO,EO分别为AB,AC的垂直平分线,则∠BOC的度数是
如图,△ABC中,∠A=70°,DO,EO分别为AB,AC的垂直平分线,则∠BOC的度数是