题目内容
9．实数$\sqrt{2}$，$\root{3}{8}$，0，$-\frac{3}{5}π$，$\sqrt{9}$，$-\frac{1}{3}$，（π-2）0，0.3131131113…（相邻两个3之间依次多一个1），其中无理数的个数是（ ）| A． | 4 | B． | 2 | C． | 1 | D． | 3 |
分析 根据无理数的定义，可得答案．
解答 解：$\sqrt{2}$，$-\frac{3}{5}π$，0.3131131113…（相邻两个3之间依次多一个1）是无理数，
故选：D．
点评 此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，$\sqrt{6}$，0.8080080008…（每两个8之间依次多1个0）等形式．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
19．若n满足（n-2015）2+（2016-n）2=1，则（n-2015）（2016-n）=（ ）
| A． | -1 | B． | 0 | C． | $\frac{1}{2}$ | D． | 1 |
20．
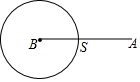如图，动点S从点A出发，沿线段AB运动至点B后，立即按原路返回，点S在运动过程中速度不变，则以点B为圆心，线段BS长为半径的圆的面积m与点S的运动时间t之间的函数关系图象大致为（ ）
如图，动点S从点A出发，沿线段AB运动至点B后，立即按原路返回，点S在运动过程中速度不变，则以点B为圆心，线段BS长为半径的圆的面积m与点S的运动时间t之间的函数关系图象大致为（ ）| A． |  | B． |  | C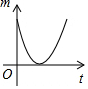． |  | D． |  |
17．
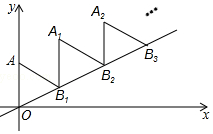如图，放置的△OAB1，△B1A1B2，△B2A2B3，…都是边长为2的等边三角形，边AO在Y轴上，点B1、B2、B3…都在直线y=$\frac{\sqrt{3}}{3}$x上，则点A2016的坐标为（ ）
如图，放置的△OAB1，△B1A1B2，△B2A2B3，…都是边长为2的等边三角形，边AO在Y轴上，点B1、B2、B3…都在直线y=$\frac{\sqrt{3}}{3}$x上，则点A2016的坐标为（ ）| A． | （2016$\sqrt{3}$，2018） | B． | （2016$\sqrt{3}$，2016） | C． | （2016，2016$\sqrt{3}$） | D． | （2016，2018$\sqrt{3}$） |
14．分式方程$\frac{4}{x-3}$-$\frac{1}{x}$=0的根是（ ）
| A． | -1 | B． | 1 | C． | 3 | D． | 0 |
1．下列计算中正确的是（ ）
| A． | a+a2=2a2 | B． | 2a•a=2a2 | C． | （2a2）2=2a4 | D． | 6a3-3a2=3a6 |
18．春节期间嘉嘉去距家10千米的电影院看电影，计划骑自行车和坐公交车两种方式，已知汽车的速度是骑车速度的2倍，若坐公交车可以从家晚15分钟出发恰好赶上公交车，结果与骑自行车同时到达，设骑车学生的速度为x千米/小时，则所列方程正确的是（ ）
| A． | $\frac{10}{x}$-$\frac{10}{2x}$=15 | B． | $\frac{10}{2x}$-$\frac{10}{x}$=15 | C． | $\frac{10}{x}$-$\frac{10}{2x}$=$\frac{1}{4}$ | D． | $\frac{10}{2x}$-$\frac{10}{x}$=$\frac{1}{4}$ |