题目内容
10. 如图,在四边形ABCD中,CB=CD,AC平分∠BCD.已知∠BCD=130°,∠D=75°,求∠B和∠DAB的度数.
如图,在四边形ABCD中,CB=CD,AC平分∠BCD.已知∠BCD=130°,∠D=75°,求∠B和∠DAB的度数.
分析 利用全等三角形的判定定理易得△ACD≌△ACB,再利用全等三角形的性质可得∠B=∠D,由四边形的内角和为360°可得∠DAB.
解答 解:连接AC,
∵AC平分∠BCD,
∴∠ACD=∠ACB,
在△ACD与△ACB中,
$\left\{\begin{array}{l}{CD=CB}\\{∠ACD=∠ACB}\\{AC=AC}\end{array}\right.$,
∴△ACD≌△ACB(SAS),
∴∠B=∠D=75°,
∴∠DAB=360°-75°-75°-130°=80°.
点评 本题主要考查了全等三角形的判定及性质定理,综合运用全等三角形的判定及性质定理是解答此题的关键.

练习册系列答案
相关题目
20.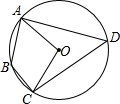 如图,四边形ABCD内接于⊙O,若∠B=130°,则∠AOC的大小是( )
如图,四边形ABCD内接于⊙O,若∠B=130°,则∠AOC的大小是( )
 如图,四边形ABCD内接于⊙O,若∠B=130°,则∠AOC的大小是( )
如图,四边形ABCD内接于⊙O,若∠B=130°,则∠AOC的大小是( )| A. | 130° | B. | 120° | C. | 110° | D. | 100° |
 如图,在△ABC中,BC=AC,将△ABC沿CD折叠(D在AB上),使得点A与点B恰好重合,如果AB=8cm,则BD=4cm.
如图,在△ABC中,BC=AC,将△ABC沿CD折叠(D在AB上),使得点A与点B恰好重合,如果AB=8cm,则BD=4cm.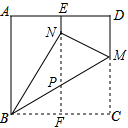 在一张边长为1的正方形纸片ABCD中,对折的折痕为EF,再将点C折到折痕EF上,落在点N的位置,折痕为BH,则EN的长为$\frac{2-\sqrt{3}}{2}$.
在一张边长为1的正方形纸片ABCD中,对折的折痕为EF,再将点C折到折痕EF上,落在点N的位置,折痕为BH,则EN的长为$\frac{2-\sqrt{3}}{2}$.