题目内容
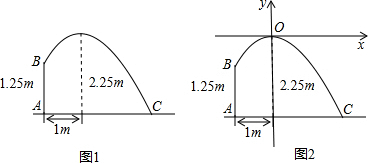
2.现有一抛物线型隧道,地面宽AB=4m,顶部C离地面高度为4.4m,现有一辆载满货物的汽车欲穿过隧道,货物顶点距离地面2.8m,装货宽度为2.4m,请通过计算,判断这辆汽车能否顺利通过隧道?分析 先过AB的中点作AB的垂直平分线建立直角坐标系,得出点A、B、C的坐标,用待定系数法即可求出过此三点的抛物线解析式,判断点(-1.2,2.8)或点(1.2,2.8)与抛物线的关系即可.
解答  解:过AB的中点作AB的垂直平分线建立直角坐标系.
解:过AB的中点作AB的垂直平分线建立直角坐标系.
点A、B、C的坐标分别为 A(-2,0),B(2,0),C(0,4.4),
设抛物线的方程为y=ax2+bx+c,
将此三点坐标代入抛物线方程得,$\left\{\begin{array}{l}{0=4a-2b+c}\\{0=4a+2b+c}\\{c=4.4}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{a=-1.1}\\{b=0}\\{c=4.4}\end{array}\right.$,
故此抛物线的解析式为:y=-1.1x2+4.4,
∵货物顶点距地面2.8米,装货宽度为2.4,
∴只要判断点(-1.2,2.8)或点(1.2,2.8)与抛物线的关系即可,
将x=1.2代入抛物线方程得 y=2.816>2.8,
∴(-1.2,2.8)或点(1.2,2.8)都在抛物线内.
∴能够通过.
点评 本题考查的是二次函数的应用,涉及到用待定系数法求二次函数的解析式及点的坐标、二次函数图象的性质,根据题意求出二次函数的解析式是解答此题的关键.

练习册系列答案
相关题目
 如图,以扇形OAB的顶点为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(4,0).若抛物线y=$\frac{1}{4}$x2+k,与扇形OAB的边界总有两个公共点,则实数k的取值范围是-4<k<1.
如图,以扇形OAB的顶点为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(4,0).若抛物线y=$\frac{1}{4}$x2+k,与扇形OAB的边界总有两个公共点,则实数k的取值范围是-4<k<1. 如图,在四边形ABCD中,CB=CD,AC平分∠BCD.已知∠BCD=130°,∠D=75°,求∠B和∠DAB的度数.
如图,在四边形ABCD中,CB=CD,AC平分∠BCD.已知∠BCD=130°,∠D=75°,求∠B和∠DAB的度数.
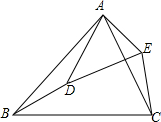 已知:如图,在△ABC和△ADE中,∠BAC=∠DAE,∠ABC=∠ADE.
已知:如图,在△ABC和△ADE中,∠BAC=∠DAE,∠ABC=∠ADE.