题目内容
19.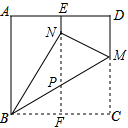 在一张边长为1的正方形纸片ABCD中,对折的折痕为EF,再将点C折到折痕EF上,落在点N的位置,折痕为BH,则EN的长为$\frac{2-\sqrt{3}}{2}$.
在一张边长为1的正方形纸片ABCD中,对折的折痕为EF,再将点C折到折痕EF上,落在点N的位置,折痕为BH,则EN的长为$\frac{2-\sqrt{3}}{2}$.
分析 由翻折的性质可知BN=BC=1,BF=$\frac{1}{2}$,在Rt△BFN中由勾股定理可求得NF=$\frac{\sqrt{3}}{2}$,最后根据EN=EF-NF求解即可.
解答 解;由翻折的性质可知:BN=BC=1,BF=$\frac{1}{2}BC=\frac{1}{2}×1=\frac{1}{2}$.
在Rt△BFN中,NF=$\sqrt{B{N}^{2}-B{F}^{2}}$=$\sqrt{{1}^{2}-(\frac{1}{2})^{2}}$=$\frac{\sqrt{3}}{2}$.
EN=EF-NF=1-$\frac{\sqrt{3}}{2}$=$\frac{2-\sqrt{3}}{2}$.
故答案为:$\frac{2-\sqrt{3}}{2}$.
点评 本题主要考查的是翻折的性质、勾股定理的应用,求得NF的长是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.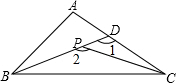 如图,P是△ABC内一点,延长CP交AB于D,则下列不等式成立的是( )
如图,P是△ABC内一点,延长CP交AB于D,则下列不等式成立的是( )
 如图,P是△ABC内一点,延长CP交AB于D,则下列不等式成立的是( )
如图,P是△ABC内一点,延长CP交AB于D,则下列不等式成立的是( )| A. | ∠2>∠A>∠1 | B. | ∠2>∠1>∠A | C. | ∠1>∠A>∠2 | D. | ∠A>∠1>∠2 |
9. 如图,AD、BC相交于点O,AB∥CD,若$\frac{AO}{OD}=\frac{2}{3}$,则$\frac{AB}{CD}$的值是( )
如图,AD、BC相交于点O,AB∥CD,若$\frac{AO}{OD}=\frac{2}{3}$,则$\frac{AB}{CD}$的值是( )
 如图,AD、BC相交于点O,AB∥CD,若$\frac{AO}{OD}=\frac{2}{3}$,则$\frac{AB}{CD}$的值是( )
如图,AD、BC相交于点O,AB∥CD,若$\frac{AO}{OD}=\frac{2}{3}$,则$\frac{AB}{CD}$的值是( )| A. | $\frac{2}{5}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{9}$ |
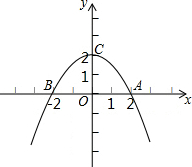 已知如图所示,抛物线y=-$\frac{1}{2}$x2+m-3与x轴交于A,B 两点.且OA=OC.求:
已知如图所示,抛物线y=-$\frac{1}{2}$x2+m-3与x轴交于A,B 两点.且OA=OC.求: 如图,在四边形ABCD中,CB=CD,AC平分∠BCD.已知∠BCD=130°,∠D=75°,求∠B和∠DAB的度数.
如图,在四边形ABCD中,CB=CD,AC平分∠BCD.已知∠BCD=130°,∠D=75°,求∠B和∠DAB的度数.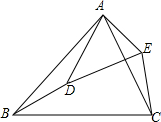 已知:如图,在△ABC和△ADE中,∠BAC=∠DAE,∠ABC=∠ADE.
已知:如图,在△ABC和△ADE中,∠BAC=∠DAE,∠ABC=∠ADE.