题目内容
20.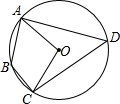 如图,四边形ABCD内接于⊙O,若∠B=130°,则∠AOC的大小是( )
如图,四边形ABCD内接于⊙O,若∠B=130°,则∠AOC的大小是( )| A. | 130° | B. | 120° | C. | 110° | D. | 100° |
分析 先根据圆内接四边形的性质得到∠D=180°-∠B=50°,然后根据圆周角定理求∠AOC.
解答 解:∵∠B+∠D=180°,
∴∠D=180°-130°=50°,
∴∠AOC=2∠D=100°.
故选D.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了圆内接四边形的性质.

练习册系列答案
相关题目
5. 实数x、y、z在数轴上的位置如图所示,则下列关系正确的是( )
实数x、y、z在数轴上的位置如图所示,则下列关系正确的是( )
 实数x、y、z在数轴上的位置如图所示,则下列关系正确的是( )
实数x、y、z在数轴上的位置如图所示,则下列关系正确的是( )| A. | x+y+z>0 | B. | x+y+z<0 | C. | xy<yz | D. | xy<xz |
9. 如图,AD、BC相交于点O,AB∥CD,若$\frac{AO}{OD}=\frac{2}{3}$,则$\frac{AB}{CD}$的值是( )
如图,AD、BC相交于点O,AB∥CD,若$\frac{AO}{OD}=\frac{2}{3}$,则$\frac{AB}{CD}$的值是( )
 如图,AD、BC相交于点O,AB∥CD,若$\frac{AO}{OD}=\frac{2}{3}$,则$\frac{AB}{CD}$的值是( )
如图,AD、BC相交于点O,AB∥CD,若$\frac{AO}{OD}=\frac{2}{3}$,则$\frac{AB}{CD}$的值是( )| A. | $\frac{2}{5}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{9}$ |
 如图,在四边形ABCD中,CB=CD,AC平分∠BCD.已知∠BCD=130°,∠D=75°,求∠B和∠DAB的度数.
如图,在四边形ABCD中,CB=CD,AC平分∠BCD.已知∠BCD=130°,∠D=75°,求∠B和∠DAB的度数.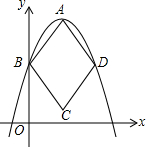 如图,在平面直角坐标系中,菱形ABCD的三个顶点A,B,D均在抛物线y=ax2-4ax+3(a<0)上.若点A是抛物线的顶点,点B是抛物线与y轴的交点,则点D的坐标为(4,3).
如图,在平面直角坐标系中,菱形ABCD的三个顶点A,B,D均在抛物线y=ax2-4ax+3(a<0)上.若点A是抛物线的顶点,点B是抛物线与y轴的交点,则点D的坐标为(4,3).


