题目内容
7.如图所示,在矩形纸片ABCD中,E,G为AB边上两点,且AE=EG=GB;F,H为CD边上两点,且DF=FH=HC.沿虚线EF折叠,使点A落在点G上,点D落在点H上;然后再沿虚线GH折叠,使B落在点E上,点C落在点F上.叠完后,剪一个直径在EF上的半圆,再展开,则展开后的图形为( )
| A. | 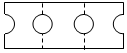 | B. | 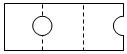 | C. | 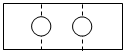 | D. | 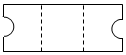 |
分析 严格按照图中的方法亲自动手操作一下,即可很直观地呈现出来.
解答 解:∵在矩形纸片ABCD中,E,G为AB边上两点,且AE=EG=GB;F,H为CD边上两点,且DF=FH=HC,
∴四边形AEFD,EGHF,GBCH是三个全等的矩形.
现在把矩形ABCD三等分,标上字母;
严格按上面方法操作,剪一个直径在EF上的半圆,
展开后实际是从矩形ABCD的一条三等分线EF处剪去一个圆,从一边BC上剪去半个圆.
故选B.
点评 本题考查了剪纸问题,学生的动手能力及空间想象能力.对于此类问题,学生只要亲自动手操作,答案就会很直观地呈现.

练习册系列答案
相关题目
17.若关于x的方程kx2+(k+1)x+1=0有两个相等的实数根,则次方程的解为( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
18.已知平行四边形ABCD中,∠B=5∠A,则∠C=( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
15. 若∠1与∠2互补,∠3=130°,则∠4等于( )
若∠1与∠2互补,∠3=130°,则∠4等于( )
 若∠1与∠2互补,∠3=130°,则∠4等于( )
若∠1与∠2互补,∠3=130°,则∠4等于( )| A. | 75° | B. | 50° | C. | 45≤ | D. | 135° |
12. 如图,a∥b,直线AB分别交a、b于A、B两点,点C在直线b上,且∠1=∠2,则下列结论正确的是( )
如图,a∥b,直线AB分别交a、b于A、B两点,点C在直线b上,且∠1=∠2,则下列结论正确的是( )
 如图,a∥b,直线AB分别交a、b于A、B两点,点C在直线b上,且∠1=∠2,则下列结论正确的是( )
如图,a∥b,直线AB分别交a、b于A、B两点,点C在直线b上,且∠1=∠2,则下列结论正确的是( )| A. | ∠1=∠ABC | B. | ∠1=∠ACB | C. | ∠ABC=∠ACB | D. | ∠2=∠ABC |
19.以下列所给线段长为三边,能构成三角形的是( )
| A. | 1cm、2cm、3cm | B. | 3cm、4cm、6cm | C. | 1cm、1cm、3cm | D. | 2cm、3cm、7cm |
16.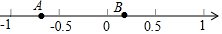 如图,在数轴上,点A和点B对应的数分别是a和b,考察结论:甲:-ab<$\frac{1}{2}$,乙:a+b>-1,丙:-a<b,丁:$\frac{a}{b}$>-2,其中正确的是( )
如图,在数轴上,点A和点B对应的数分别是a和b,考察结论:甲:-ab<$\frac{1}{2}$,乙:a+b>-1,丙:-a<b,丁:$\frac{a}{b}$>-2,其中正确的是( )
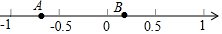 如图,在数轴上,点A和点B对应的数分别是a和b,考察结论:甲:-ab<$\frac{1}{2}$,乙:a+b>-1,丙:-a<b,丁:$\frac{a}{b}$>-2,其中正确的是( )
如图,在数轴上,点A和点B对应的数分别是a和b,考察结论:甲:-ab<$\frac{1}{2}$,乙:a+b>-1,丙:-a<b,丁:$\frac{a}{b}$>-2,其中正确的是( )| A. | 甲、乙 | B. | 甲、丙 | C. | 丙、丁 | D. | 乙、丁 |
17. 如图所示,添加一个条件后可得AB∥CD,则添加这个条件不能是( )
如图所示,添加一个条件后可得AB∥CD,则添加这个条件不能是( )
 如图所示,添加一个条件后可得AB∥CD,则添加这个条件不能是( )
如图所示,添加一个条件后可得AB∥CD,则添加这个条件不能是( )| A. | ∠A=∠2 | B. | ∠A=∠1 | C. | ∠B=∠2 | D. | ∠A+∠ACD=180° |
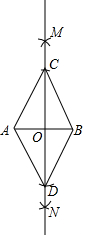 小明在白纸上作一个菱形,他按如下步骤:
小明在白纸上作一个菱形,他按如下步骤: