题目内容
15. 若∠1与∠2互补,∠3=130°,则∠4等于( )
若∠1与∠2互补,∠3=130°,则∠4等于( )| A. | 75° | B. | 50° | C. | 45≤ | D. | 135° |
分析 由平行线的判定定理证得a∥b;然后根据平行线的性质、对顶角相等即可求得∠4的度数.
解答 解:∵∠1与∠2互补,
∴a∥b(同旁内角互补,两直线平行),
∴∠4+∠5=180°(两直线平行,同旁内角互补);
又∵∠3=∠5(对顶角相等),∠3=130°(已知),
∴∠4=50°.
故选B.
点评 本题考查了平行线的判定与性质.解答此题的关键是注意平行线的性质(两直线平行,同旁内角互补)和判定定理(同旁内角互补,两直线平行)的综合运用.

练习册系列答案
相关题目
5.下列语句正确的是( )
| A. | 一条直线可以看成一个平角 | |
| B. | 周角是一条射线 | |
| C. | 角是由一条射线旋转而成的 | |
| D. | 角是由公共端点的两条射线组成的图形 |
3.下列命题:(1)如果AC=BC,那么点C是线段AB的中点;(2)相等的两个角是对顶角;(3)直角三角形的两个锐角互余;(4)同位角相等;(5)两点之间,直线最短.其中真命题的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.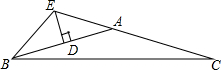 如图,△ABC中,AB=AC,AB的垂直平分线交AB于点D,交CA的延长线于点E,∠EBC=42°,则∠BAC=( )
如图,△ABC中,AB=AC,AB的垂直平分线交AB于点D,交CA的延长线于点E,∠EBC=42°,则∠BAC=( )
 如图,△ABC中,AB=AC,AB的垂直平分线交AB于点D,交CA的延长线于点E,∠EBC=42°,则∠BAC=( )
如图,△ABC中,AB=AC,AB的垂直平分线交AB于点D,交CA的延长线于点E,∠EBC=42°,则∠BAC=( )| A. | 159° | B. | 154° | C. | 152° | D. | 138° |
5.下列二次根式中,最简二次根式的是( )
| A. | $\sqrt{3{a^2}}$ | B. | $\sqrt{11a}$ | C. | $\sqrt{12}$ | D. | $\sqrt{\frac{1}{3}}$ |
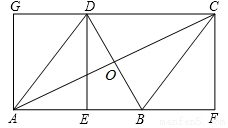 如图,在矩形AFCG中,BD垂直平分对角线AC,交CG于D,交AF于B,交AC于O,连接AD,BC.
如图,在矩形AFCG中,BD垂直平分对角线AC,交CG于D,交AF于B,交AC于O,连接AD,BC.