题目内容
18．已知平行四边形ABCD中，∠B=5∠A，则∠C=（ ）| A． | 30° | B． | 60° | C． | 120° | D． | 150° |
分析 首先根据平行四边形的性质可得∠A=∠C，∠A+∠B=180°，再由已知条件计算出∠A的度数，即可得出∠C的度数．
解答 解：∵四边形ABCD是平行四边形，
∴AD∥BC，∠A=∠C，
∴∠A+∠B=180°，
∵∠B=5∠A，
∴∠A+5∠A=180°，
解得：∠A=30°，
∴∠C=30°，
故选：A．
点评 此题主要考查了平行四边形的性质，关键是掌握平行四边形两组对边分别平行，两组对角分别相等．
练习册系列答案
相关题目
8．如果（a-1）x2+ax+a2-1=0是关于x的一元二次方程，那么必有（ ）
| A． | a≠0 | B． | a≠1 | C． | a≠-1 | D． | a=±-1 |
9．若a2-2a-2=0，则（a-1）2=（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
13．由$\frac{x}{3}$-y=6，可以得到用x表示y的式子是（ ）
| A． | x=18-y | B． | x=18-3y | C． | y=$\frac{x}{3}$-6 | D． | y=$\frac{x}{3}$+6 |
3．下列命题：（1）如果AC=BC，那么点C是线段AB的中点；（2）相等的两个角是对顶角；（3）直角三角形的两个锐角互余；（4）同位角相等；（5）两点之间，直线最短．其中真命题的个数有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
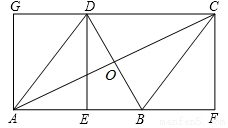如图，在矩形AFCG中，BD垂直平分对角线AC，交CG于D，交AF于B，交AC于O，连接AD，BC．
8．
如图，AD是△ABC的高，AD=BD，DE=DC，∠BAC=75°，则∠ABE的度数是（ ）
如图，AD是△ABC的高，AD=BD，DE=DC，∠BAC=75°，则∠ABE的度数是（ ）| A． | 10° | B． | 15° | C． | 30° | D． | 45° |