题目内容
已知数x=
0,求证:x-25是完全平方数.
| ||
| n个0 |
| ||
| n+1个0 |
考点:完全平方数
专题:
分析:将x展开,化为(10n+2)2+2•10n+2•5+50,减去25后可得完全平方式(10n+2)2+2•10n+2•5+25,即x-25=(10n+2+5)2.
解答:解:∵x=
0
=100…00(2n+4个0)+100…00(n+3个0)+50
=102n+4+10n+3+50
=(10n+2)2+2•10n+2•5+50.
∴x-25
=(10n+2)2+2•10n+2•5+50-25
=(10n+2)2+2•10n+2•5+25
=(10n+2+5)2.
故x-25是完全平方数.
| ||
| n个0 |
| ||
| n+1个0 |
=100…00(2n+4个0)+100…00(n+3个0)+50
=102n+4+10n+3+50
=(10n+2)2+2•10n+2•5+50.
∴x-25
=(10n+2)2+2•10n+2•5+50-25
=(10n+2)2+2•10n+2•5+25
=(10n+2+5)2.
故x-25是完全平方数.
点评:此题考查了完全平方式的定义,将原数变形为完全平方公式的形式是解题的关键.

练习册系列答案
相关题目
 如图,AB是⊙O直径,弦CD与AB相交于点E,∠ACD=52°,∠ADC=26°.求∠CEB的度数.
如图,AB是⊙O直径,弦CD与AB相交于点E,∠ACD=52°,∠ADC=26°.求∠CEB的度数.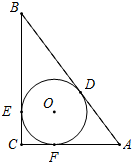 如图,在△ABC中,∠C=90°,⊙O是△ABC的内切圆,切点分别为D,E,F,若BD=6,AD=4,求⊙O的半径r.
如图,在△ABC中,∠C=90°,⊙O是△ABC的内切圆,切点分别为D,E,F,若BD=6,AD=4,求⊙O的半径r. 某水果种植户去年共摘得一级柑橘4000kg,并计划在今年的某个月内全部售出.由于受季节等因素影响,每千克一级柑橘的月平均售价如图所示(图中各点在同一直线上).自今年一月份开始,柑橘每多保存一个月将减少200kg,同时需要花费0.02元/kg的保存费.
某水果种植户去年共摘得一级柑橘4000kg,并计划在今年的某个月内全部售出.由于受季节等因素影响,每千克一级柑橘的月平均售价如图所示(图中各点在同一直线上).自今年一月份开始,柑橘每多保存一个月将减少200kg,同时需要花费0.02元/kg的保存费.