题目内容
 如图,∠MON=90°,定长线段AB=10,两个端点分别在OM、ON上滑动,则AB的中点P运动的路径长为多少?
如图,∠MON=90°,定长线段AB=10,两个端点分别在OM、ON上滑动,则AB的中点P运动的路径长为多少?考点:弧长的计算,直角三角形斜边上的中线,轨迹
专题:
分析:根据勾股定理,可得a2+b2=100,根据线段中点的性质,可得P点坐标,根据(
)2+(
)2的值,可得P点的路径,根据弧长公式,可得答案.
| a |
| 2 |
| b |
| 2 |
解答:解:设A(a,0),B(0,b),P(
,
),
由勾股定理,得
a2+b2=100.
(
)2+(
)2=
=25,
以O为圆心,以5为半径的圆周的
,
AB的中点P运动的路径长
=
.
| a |
| 2 |
| b |
| 2 |
由勾股定理,得
a2+b2=100.
(
| a |
| 2 |
| b |
| 2 |
| a2+b2 |
| 4 |
以O为圆心,以5为半径的圆周的
| 1 |
| 4 |
AB的中点P运动的路径长
| 2π×5 |
| 4 |
| 5π |
| 2 |
点评:本题考查了弧长公式,利用了线段中点的性质,圆弧与圆周的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,正方形ABCD的边长为a cm,剪去4个角后成为正八边形,则正八边形的边长为多少?面积为多少?
如图,正方形ABCD的边长为a cm,剪去4个角后成为正八边形,则正八边形的边长为多少?面积为多少?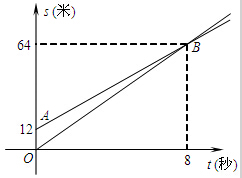 如图,图中两条射线分别表示甲、乙两名同学运动的路程s(米)和时间t(秒)的关系图象,已知甲的速度比乙快.下面么给出四种说法:
如图,图中两条射线分别表示甲、乙两名同学运动的路程s(米)和时间t(秒)的关系图象,已知甲的速度比乙快.下面么给出四种说法: 如图为二次函数y=ax2+bx+c(a≠0)的图象,下面四条信息:①abc>0;②4a+c<2b;③4ac-b2<0;④3b+2c<0,其中正确信息的个数是( )
如图为二次函数y=ax2+bx+c(a≠0)的图象,下面四条信息:①abc>0;②4a+c<2b;③4ac-b2<0;④3b+2c<0,其中正确信息的个数是( ) 如图,点C和点D在线段AB上,AE∥BF,AE=FB,AC=DB,连接EC、ED、FC、FD.
如图,点C和点D在线段AB上,AE∥BF,AE=FB,AC=DB,连接EC、ED、FC、FD.