Question

如图，点C和点D在线段AB上，AE∥BF，AE=FB，AC=DB，连接EC、ED、FC、FD．
（1）求证：四边形ECFD是平行四边形；
（2）若CE=CF，∠AED=90°，AE=20，ED=15，求AB的长．

Answer 1

考点：平行四边形的判定与性质,全等三角形的判定与性质

专题：

分析：（1）首先连接AF，BE，EF交AB于点O，由AE∥BF，AE=FB，可证得四边形AFBE是平行四边形，则可得OA=OB，OE=OF，继而证得OC=OD，即可证得四边形ECFD是平行四边形；
（2）由CE=CF，可得四边形ECFD是菱形，又由∠AED=90°，AE=20，ED=15，易求得AD的长，易证得△AOE∽△AED，然后由相似三角形的对应边成比例，求得答案．

解答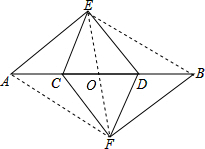：（1）证明：连接AF，BE，EF交AB于点O，
∵AE∥BF，AE=FB，
∴四边形AFBE是平行四边形，
∴OA=OB，OE=OF，
∵AC=DB，
∴OC=OD，
∴四边形ECFD是平行四边形；

（2）解：∵CE=CF，四边形ECFD是平行四边形，
∴?ECFD是菱形，
∴EF⊥CD，
∵∠AED=90°，AE=20，ED=15，
∴AD=

AE2+ED2

=25，
∵∠AOE=∠AED=90°，∠OAE=∠EAD，
∴△AOE∽△AED，
∴

OE

ED

=

AE

AD

，
∴

OE

15

=

20

25

，
∴OE=12，
∴OC=OD=

DE2-OE2

=9，
∴AC=BD=AD-CD=25-18=7，
∴AB=AD+BD=25+7=32．

点评：此题考查了平行四边形的判定与性质、相似三角形的判定与性质以及勾股定理．此题难度适中，注意掌握数形结合思想的应用．