题目内容
已知二次函数y=2x2+x+m的图象与x轴有唯一交点,则当-1≤x≤0时,y的取值范围是 .
考点:抛物线与x轴的交点
专题:
分析:令y=0得一元二次方程,由条件可知其判别式等于0可求得m,再利用二次函数的增减性求得y的范围.
解答:解:在y=2x2+x+m中,令y=0可得2x2+x+m=0,
∵二次函数y=2x2+x+m的图象与x轴有唯一交点,
∴△=1-8m=0,解得m=
,
∴二次函数为y=2x2+x+
,
其对称轴为x=-
,
当-1≤x≤-
时,y随x的增大而减小,当x=-
时,y有最小0,当x=-1时,y有最大值
;
当-
≤x≤0时,y随x的增大而增大,当x=-
时,y有最小0,当x=0时,y有最大值
;
∴当-1≤x≤0时,y的取值范围是0≤y≤
,
故答案为:0≤y≤
.
∵二次函数y=2x2+x+m的图象与x轴有唯一交点,
∴△=1-8m=0,解得m=
| 1 |
| 8 |
∴二次函数为y=2x2+x+
| 1 |
| 8 |
其对称轴为x=-
| 1 |
| 4 |
当-1≤x≤-
| 1 |
| 4 |
| 1 |
| 4 |
| 9 |
| 8 |
当-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 8 |
∴当-1≤x≤0时,y的取值范围是0≤y≤
| 9 |
| 8 |
故答案为:0≤y≤
| 9 |
| 8 |
点评:本题主要考查二次函数与x轴的交点及增减性,掌握二次函数与对应的一元二次方程的关系及对称轴两侧的增减性是解题的关键.

练习册系列答案
相关题目
在平面直角坐标系中,点(3,-5)关于x轴的对称点在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
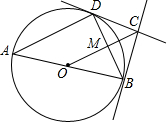 如图,AB为⊙O的直径,BC⊥AB,OC过BD中点M,求证:CD是⊙O的切线.
如图,AB为⊙O的直径,BC⊥AB,OC过BD中点M,求证:CD是⊙O的切线.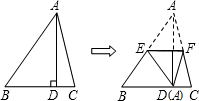 如图,在△ABC中,AB=12,AC=10,BC=9,AD⊥BC.将△ABC按如图所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为
如图,在△ABC中,AB=12,AC=10,BC=9,AD⊥BC.将△ABC按如图所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为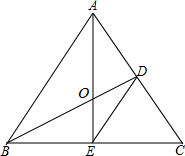 如图,△ABC是等边三角形,BD⊥AC,AE⊥BC,垂足分别为D、E,AE、BD相交于点O,连接DE.
如图,△ABC是等边三角形,BD⊥AC,AE⊥BC,垂足分别为D、E,AE、BD相交于点O,连接DE. 如图,∠MON=90°,定长线段AB=10,两个端点分别在OM、ON上滑动,则AB的中点P运动的路径长为多少?
如图,∠MON=90°,定长线段AB=10,两个端点分别在OM、ON上滑动,则AB的中点P运动的路径长为多少?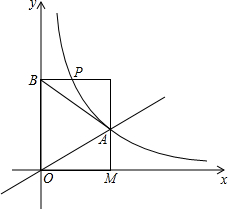 如图,在平面直角坐标系中,正比例函数y=
如图,在平面直角坐标系中,正比例函数y= 已知∠ABE:∠CBE=1:4,BD平分∠ABC,∠DBE=45°,求∠ABC的度数.
已知∠ABE:∠CBE=1:4,BD平分∠ABC,∠DBE=45°,求∠ABC的度数.