��Ŀ����
5����ѧ���˶�Ԫһ�η�����Ľⷨ��������ʦ��д����һ����Ŀ��$\left\{\begin{array}{l}{\frac{x+y}{6}+\frac{x-y}{10}=3��}\\{\frac{x+y}{6}-\frac{x-y}{10}=-1��}\end{array}\right.$�����������������С����С�ա�С��������һ��������Ƿֱ�д����һ�ַ�����
С������ԭ������������$\left\{\begin{array}{l}{8x+2y=90��}\\{2x+8y=-30��}\end{array}\right.$
�ܡ�4-�۵�30y=-210������y=-7
��y=-7����۵�8x=104������x=13��
��$\left\{\begin{array}{l}{x=13}\\{y=-7}\end{array}\right.$
С�գ���$\frac{x+y}{6}$=m��$\frac{x-y}{10}$=n����$\left\{\begin{array}{l}{m+n=3��}\\{m-n=-1��}\end{array}\right.$
��+�ܵ�m=1��
��-�ܵ�m=2��
��$\left\{\begin{array}{l}{\frac{x+y}{6}=1}\\{\frac{x-y}{10}=2}\end{array}\right.$������$\left\{\begin{array}{l}{x+y=6}\\{x-y=20}\end{array}\right.$������$\left\{\begin{array}{l}{x=13}\\{y=-7}\end{array}\right.$��
С������+�ڵ�$\frac{2��x+y��}{6}$=2����x+y=6����
��-�ڵ�$\frac{2��x-y��}{10}$=4����x-y=20����
�ۢ���ɷ������x=13
��-�ܵ�y=-7����$\left\{\begin{array}{l}{x=13}\\{y=-7}\end{array}\right.$��
��ʦ�����dz����ˣ��ر���С�յķ������أ���С�յ����ַ���������Ԫ���������û�Ԫ�������з�������
$\left\{\begin{array}{l}{\frac{3x-2y}{6}+\frac{2x+3y}{7}=1}\\{\frac{3x-2y}{6}-\frac{2x+3y}{7}=5}\end{array}\right.$��
���� ��$\frac{3x-2y}{6}$=m��$\frac{2x+3y}{7}$=n�����������������m��n��ֵ������ȷ����x��y��ֵ��
��� �⣺��$\frac{3x-2y}{6}$=m��$\frac{2x+3y}{7}$=n��
�����������ã�$\left\{\begin{array}{l}{m+n=1��}\\{m-n=5��}\end{array}\right.$��
��+�ڵã�2m=6����m=3��
��-�ڵã�2n=-4����n=-2��
��$\left\{\begin{array}{l}{\frac{3x-2y}{6}=3}\\{\frac{2x+3y}{7}=-2}\end{array}\right.$��
�����ã�$\left\{\begin{array}{l}{3x-2y=18}\\{2x+3y=-14}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=2}\\{y=-6}\end{array}\right.$��
���� ���⿼���˽��Ԫһ�η����飬��������Ԫ��˼�룬��Ԫ�ķ����У�������Ԫ����Ӽ���Ԫ����

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
20��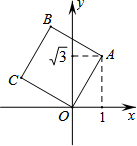 ��ͼ����������OABC����ƽ��ֱ������ϵ�У�O��ԭ�㣬A������Ϊ��1��$\sqrt{3}$�������C������Ϊ��������
��ͼ����������OABC����ƽ��ֱ������ϵ�У�O��ԭ�㣬A������Ϊ��1��$\sqrt{3}$�������C������Ϊ��������
 ��ͼ����������OABC����ƽ��ֱ������ϵ�У�O��ԭ�㣬A������Ϊ��1��$\sqrt{3}$�������C������Ϊ��������
��ͼ����������OABC����ƽ��ֱ������ϵ�У�O��ԭ�㣬A������Ϊ��1��$\sqrt{3}$�������C������Ϊ��������| A�� | ��-1��$\sqrt{3}$�� | B�� | ��-$\sqrt{3}$��1�� | C�� | ��-2��1�� | D�� | ��-1��2�� |
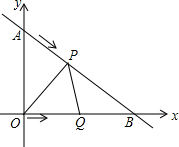 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-$\frac{3}{4}$x+3�������ύ��A��B���㣬��P��Q�ֱ�ΪAB�ߣ�OB���ϵĶ��㣬����ͬʱ�ֱ�ӵ�A����O��ÿ��1����λ�ٶ����յ�B�����ƶ�����һ���㵽���յ�ʱ��һ����Ҳֹͣ�ƶ������ƶ�ʱ��Ϊt�룮
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-$\frac{3}{4}$x+3�������ύ��A��B���㣬��P��Q�ֱ�ΪAB�ߣ�OB���ϵĶ��㣬����ͬʱ�ֱ�ӵ�A����O��ÿ��1����λ�ٶ����յ�B�����ƶ�����һ���㵽���յ�ʱ��һ����Ҳֹͣ�ƶ������ƶ�ʱ��Ϊt�룮