题目内容
14.解下列不等式,并把它们的解集在数轴上表示出来:(1)3(2x+7)>23;
(2)12-4(3x-1)≤2(2x-16);
(3)$\frac{x+3}{5}$<$\frac{2x-5}{3}$-1;
(4)$\frac{2x-1}{3}$-$\frac{3x-1}{2}$≥$\frac{5}{12}$.
分析 (1)不等式去括号,移项合并,把x系数化为1,求出解集,表示在数轴上即可;
(2)不等式去括号,移项合并,把x系数化为1,求出解集,表示在数轴上即可;
(3)不等式去分母,去括号,移项合并,把x系数化为1,求出解集,表示在数轴上即可;
(4)不等式去分母,去括号,移项合并,把x系数化为1,求出解集,表示在数轴上即可.
解答 解:(1)去括号得:6x+21>23,
解得:x>$\frac{1}{3}$,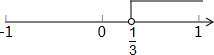 ;
;
(2)去括号得:12-12x+4≤4x-32,
移项合并得:-16x≤-48,
解得:x≥3,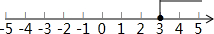 ;
;
(3)去分母得:3(x+3)<5(2x-5)-15,
去括号得:3x+9<10x-25-15,
移项合并得:7x>49,
解得:x>7, ;
;
(4)去分母得:4(2x-1)-6(3x-1)≥5,
去括号得:8x-4-18x+6≥5,
移项合并得:-10x≥3,
解得:x≤-$\frac{3}{10}$,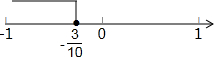
点评 此题考查了解一元一次不等式,以及在数轴上表示不等式的解集,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.一个直角三角形两条直角边的长分别为4,8,另一个和它相似的直角三角形的一条直角边为12,则另一条直角边的长为( )
| A. | 6 | B. | 24 | C. | 6或24 | D. | 6$\sqrt{5}$或$\sqrt{10}$ |
3.若实数x满足x-$\frac{1}{x}$=1,则$\frac{{x}^{2}}{{x}^{4}+{x}^{2}+1}$的值是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1±\sqrt{5}}{2}$ | D. | $\frac{1+\sqrt{5}}{2}$ |
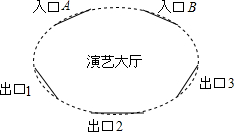 某演艺大厅有2个入口和3个出口,其示意图如下,参观者从任意一个入口进入,参观结束后从任意一个出口离开
某演艺大厅有2个入口和3个出口,其示意图如下,参观者从任意一个入口进入,参观结束后从任意一个出口离开