题目内容
13.已知y与x2成正比例,且当x=3时,y=-18,写出y与x之间的函数解析式,它是二次函数吗?分析 由于y与x2成反比例,则有y=kx2(k≠0),然后把x=3,y=-18代入即可求出k.
解答 解:∵y与x2成正比例,
∴y=kx2(k≠0),
把x=3时,y=-18代入得:-18=32•k,
∴k=-2,
∴y与x之间的函数解析式为 y=-2x2.
符合二次函数的定义,属于二次函数.
点评 本题考查了二次函数的定义,正比例函数的定义.二次函数的定义:一般地,形如y=ax2+bx+c(a、b、c是常数,a≠0)的函数,叫做二次函数.其中x、y是变量,a、b、c是常量,a是二次项系数,b是一次项系数,c是常数项.y=ax2+bx+c(a、b、c是常数,a≠0)也叫做二次函数的一般形式.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
3.把多项式2x2-18分解因式,结果正确的是( )
| A. | 2(x2-9) | B. | 2(x+9)(x-9) | C. | 2(x+3)(x-3) | D. | 2(x-3)2 |
8.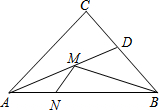 如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
 如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )| A. | $3\sqrt{2}$ | B. | 4 | C. | $4\sqrt{2}$ | D. | 6 |
2.一个直角三角形两条直角边的长分别为4,8,另一个和它相似的直角三角形的一条直角边为12,则另一条直角边的长为( )
| A. | 6 | B. | 24 | C. | 6或24 | D. | 6$\sqrt{5}$或$\sqrt{10}$ |
3.若实数x满足x-$\frac{1}{x}$=1,则$\frac{{x}^{2}}{{x}^{4}+{x}^{2}+1}$的值是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1±\sqrt{5}}{2}$ | D. | $\frac{1+\sqrt{5}}{2}$ |
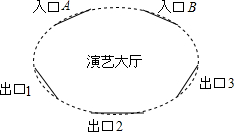 某演艺大厅有2个入口和3个出口,其示意图如下,参观者从任意一个入口进入,参观结束后从任意一个出口离开
某演艺大厅有2个入口和3个出口,其示意图如下,参观者从任意一个入口进入,参观结束后从任意一个出口离开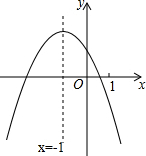 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论: