题目内容
15.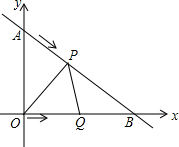 如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+3与坐标轴交于A,B两点,设P,Q分别为AB边,OB边上的动点,它们同时分别从点A,点O以每秒1个单位速度向终点B匀速移动,当一个点到达终点时另一个点也停止移动,设移动时间为t秒.
如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+3与坐标轴交于A,B两点,设P,Q分别为AB边,OB边上的动点,它们同时分别从点A,点O以每秒1个单位速度向终点B匀速移动,当一个点到达终点时另一个点也停止移动,设移动时间为t秒.(1)请写出点A,点B的坐标;
(2)试求△OPQ的面积S与移动时间t之间的函数关系式,当t为何值时,S有最大值?并求出S的最大值;
(3)试证明无论t为何值,△OPQ都不会是等边三角形;
(4)将△OPQ沿直线PQ折叠,得到△O′PQ,问:△OPQ和O′PQ能否拼成一个三角形?若能,求出点O′的坐标;若不能,请说明理由.
分析 (1)根据自变量与函数值的对应关系,可得答案;
(2)根据三角函数,可得PD的长,根据三角形的面积公式,可得函数解析式,根据二次函数的性质,可得答案;
(3)根据等边三角形的性质,可得∠POQ=∠OPQ=60°,根据等腰三角形的性质,可得∠APO=120°,再根据邻补角,可得∠QPB的度数,根据∠QPB与∠OPQ的关系,可得答案;
(4)根据轴对称的性质,可得O点关于PQ的对称点O′不在x轴上,根据四边形的定义,可得答案.
解答 解:(1)当x=0时,y=3,即A(0.3),当y=0时,-$\frac{3}{4}$x+3=0,即B(4,0);
(2)如图1:作PD⊥x轴于D.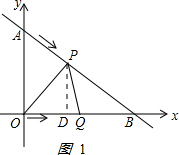 ,
,
OQ=t,AP=t,PB=5-t,
sin∠B=$\frac{AO}{AB}$=$\frac{3}{5}$,
PD=PB•sin∠B=$\frac{3}{5}$(5-t),
S=$\frac{1}{2}$OQ•PD=$\frac{1}{2}$t(5-t)=-$\frac{1}{2}$t2+$\frac{5}{2}$t,
当t=$\frac{5}{4}$时,s最大=$\frac{25}{2}$;
(3)证明:∵OP=OQ=AP=PQ,∠POQ=∠OPQ=60°,
∴∠AOP=∠PAO=30°,
∴∠APO=120°,
∴∠BPQ=60°与∠OPQ=60°矛盾,
∴∠OPQ≠60°,即△OPQ都不会是等边三角形;
(4):△OPQ和O′PQ不能拼成一个三角形,理由如下:
如图2,作PE⊥y轴于E点.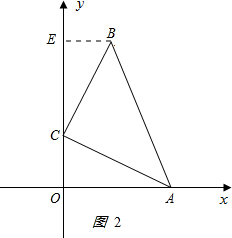 ,
,
∵AP=OQ>PE,
∴PQ∥y轴,
∴O点关于PQ的对称点O′不在x轴上,
∴O、Q、O′不在同一条直线上,
∴OPO′Q是四边形,
△OPQ和O′PQ不能拼成一个三角形.
点评 本题考查了一次函数的综合题,利用了自变量与函数值的对应关系,锐角三角函数的定义,三角形的面积公式,二次函数的性质,轴对称的性质,四边形的定义,利用反证法是解题关键.

 阅读快车系列答案
阅读快车系列答案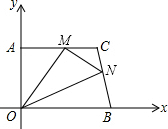 在平面直角坐标系中,直角梯形AOBC的位置如图所示,∠OAC=90°,AC∥OB,OA=4,AC=5,OB=6.M、N分别在线段AC、线段BC上运动,当△MON的面积达到最大时,存在一种使得△MON周长最小的情况,则此时点M的坐标为( )
在平面直角坐标系中,直角梯形AOBC的位置如图所示,∠OAC=90°,AC∥OB,OA=4,AC=5,OB=6.M、N分别在线段AC、线段BC上运动,当△MON的面积达到最大时,存在一种使得△MON周长最小的情况,则此时点M的坐标为( )| A. | (0,4) | B. | (3,4) | C. | ($\frac{5}{2}$,4) | D. | ($\sqrt{3}$,3) |
| A. | 2(x2-9) | B. | 2(x+9)(x-9) | C. | 2(x+3)(x-3) | D. | 2(x-3)2 |
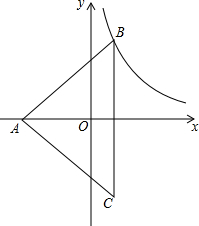 如图,等腰三角形ABC的外心与原点重合,AB=AC=10,BC=12,顶点A在x轴负半轴,顶点B在反比例函数y=$\frac{k}{x}$位于第一象限的图象上,则k的值为$\frac{21}{2}$.
如图,等腰三角形ABC的外心与原点重合,AB=AC=10,BC=12,顶点A在x轴负半轴,顶点B在反比例函数y=$\frac{k}{x}$位于第一象限的图象上,则k的值为$\frac{21}{2}$.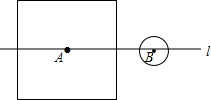 如图,直线l过边长为10的正方形中心A,且与正方形的一组对边平行,B在直线l上,AB=7,圆B的半径等于r.
如图,直线l过边长为10的正方形中心A,且与正方形的一组对边平行,B在直线l上,AB=7,圆B的半径等于r.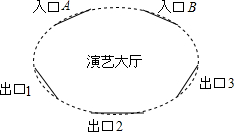 某演艺大厅有2个入口和3个出口,其示意图如下,参观者从任意一个入口进入,参观结束后从任意一个出口离开
某演艺大厅有2个入口和3个出口,其示意图如下,参观者从任意一个入口进入,参观结束后从任意一个出口离开