题目内容
8.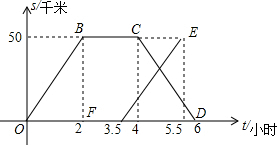 为搜集植物标本,老师带领第一组同学从学校先乘车出发,寻找到目的地,采集中,向另一组同学报告,采完后立即返回,第二组同学接到报告后,立即从学校出发,如图是两组同学与学校的距离s和离开学校的时间t之间的函数图象.(假设两组同学沿同一路线行进)
为搜集植物标本,老师带领第一组同学从学校先乘车出发,寻找到目的地,采集中,向另一组同学报告,采完后立即返回,第二组同学接到报告后,立即从学校出发,如图是两组同学与学校的距离s和离开学校的时间t之间的函数图象.(假设两组同学沿同一路线行进)(1)直接写出第一组同学离开学校的距离s和他们离开学校的时间t之间的函数关系式;
(2)求两组同学相遇时,他们与学校的距离;
(3)在两组同学行动的过程中,求第一组同学出发多少时间后与第二组同学相距12.5km?
分析 (1)利用待定系数法求解,分三种情况求函数解析式:当0≤t≤2时;当2<t<4时;当4≤t≤6时;
(2)利用得到系数法求第二组同学的函数解析式s=25t-87.5.联立s=25t-87.5与s=-25t+150得到方程组,即可解答;
(3)分两种情况讨论:当(25t-87.5)-(-25t+150)=12.5时或当(-25t+150)-(25t-87.5)=12.5时,即可解答.
解答 解:(1)当0≤t≤2时,学生乘车的速度为50÷2=25(千米/小时)
∴s=25t;
当2<t<4时,y=60;
当4≤t≤6时,设函数关系式为s=kt+b,
把(4,50),(6,0)代入得:$\left\{\begin{array}{l}{4k+b=50}\\{6k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-25}\\{b=150}\end{array}\right.$,
∴s=-25t+150,
∴第一组同学离开学校的距离s和他们离开学校的时间t之间的函数关系式为:s=$\left\{\begin{array}{l}{25t(0≤t≤2)}\\{50(2<t<4)}\\{-25t+150(4≤t≤6)}\end{array}\right.$.
(2)设第二组同学的函数解析式为s=k2t+b2,
把(3.5,0)(5.5,50)代入得:$\left\{\begin{array}{l}{{3,5k}_{2}+b=0}\\{5.5{k}_{2}+b=50}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=25}\\{{b}_{2}=-87.5}\end{array}\right.$,
∴s=25t-87.5.
联立s=25t-87.5与s=-25t+150,得:$\left\{\begin{array}{l}{s=25t-87.5}\\{s=-25t+150}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{t=4.75}\\{s=31.25}\end{array}\right.$,
∴两组同学相遇时,他们与学校的距离为31.25千米;
(3)当(25t-87.5)-(-25t+150)=12.5时,
解得:t=5,
当(-25t+150)-(25t-87.5)=12.5时,
解得:t=4.5,
∴在两组同学行动的过程中,第一组同学出发4.5小时或5小时后与第二组同学相距12.5km.
点评 本题考查了待定系数法求一次函数的解析式的运用,一次函数与一元一次方程的关系的运用,解答时求出一次函数的解析式是关键.

| A. | 40° | B. | 130° | C. | 50° | D. | 140° |
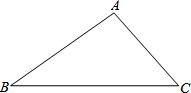 如图,△ABC中,∠B=30°,∠BAC=105°,AB=24,求△ABC的面积.
如图,△ABC中,∠B=30°,∠BAC=105°,AB=24,求△ABC的面积. 小明每天早上步行到学校上学.一天,小明从家里出发后5分钟时,他爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度沿相同路线去追小明,并在途中追上小明,设小明离开家的时间为x(分),如图图象中的线段OA表示小明从家到学校的过程中离开家的距离y1(米)与x(分)的关系;线段BP表示爸爸追赶小明时离开家的距离y2(米)与x(分)之间的关系,请分析图中的信息并解答下列问题:
小明每天早上步行到学校上学.一天,小明从家里出发后5分钟时,他爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度沿相同路线去追小明,并在途中追上小明,设小明离开家的时间为x(分),如图图象中的线段OA表示小明从家到学校的过程中离开家的距离y1(米)与x(分)的关系;线段BP表示爸爸追赶小明时离开家的距离y2(米)与x(分)之间的关系,请分析图中的信息并解答下列问题: