题目内容
9.已知最简二次根式$\sqrt{{a}^{2}-a}$与$\sqrt{4a-6}$是同类二次根式,求关于x的方程(a-2)x2+2x-3=0的解.分析 根据同类二次根式的定义知2a2-a=4a-2,据此可以求得a的值;然后将其代入所求的方程(a-2)x2+2x-3=0并解方程即可.
解答 解:∵最简二次根式$\sqrt{{a}^{2}-a}$与$\sqrt{4a-6}$是同类二次根式,
∴a2-a=4a-6,
解得:a=2或a=3,
当a=2时,关于x的方程为2x-3=0,
解得:x=$\frac{3}{2}$,
当a=3时,关于x的方程为x2+2x-3=0,
解得;x=1,x=-3,
∴关于x的方程(a-2)x2+2x-3=0的解:x=1、x=-3或x=$\frac{3}{2}$.
点评 本题考查了同类二次根式、解一元二次方程--因式分解法.解答该题时需要注意二次根式有意义的条件(被开方数是非负数).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.下列各式属于最简二次根式的有( )
| A. | $\sqrt{8}$ | B. | $\sqrt{{x}^{2}+1}$ | C. | $\sqrt{{y}^{3}}$ | D. | $\sqrt{\frac{1}{2}}$ |
4.下列方程中,是关于x的一元二次方程的是( )
| A. | 2y2+y-1=0 | B. | $\frac{1}{{x}^{2}}$-2x=1 | C. | ax2+bx+c=0 | D. | $\frac{1}{2}$x2=0 |
18.若不等式组$\left\{\begin{array}{l}x<m\\ x>11\end{array}\right.$无解,则m的取值范围是( )
| A. | m<11 | B. | m>11 | C. | m≤11 | D. | m≥11 |
19.计算:(-a2)3( )
| A. | a6 | B. | -a6 | C. | a5 | D. | -a5 |
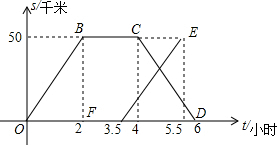 为搜集植物标本,老师带领第一组同学从学校先乘车出发,寻找到目的地,采集中,向另一组同学报告,采完后立即返回,第二组同学接到报告后,立即从学校出发,如图是两组同学与学校的距离s和离开学校的时间t之间的函数图象.(假设两组同学沿同一路线行进)
为搜集植物标本,老师带领第一组同学从学校先乘车出发,寻找到目的地,采集中,向另一组同学报告,采完后立即返回,第二组同学接到报告后,立即从学校出发,如图是两组同学与学校的距离s和离开学校的时间t之间的函数图象.(假设两组同学沿同一路线行进) 如图小明在楼上点A处测得旗杆BC顶部B的仰角为30°,测得旗杆底部C的俯角为60°,已知点A距地面高AD为12m,旗杆的高度为16 m.
如图小明在楼上点A处测得旗杆BC顶部B的仰角为30°,测得旗杆底部C的俯角为60°,已知点A距地面高AD为12m,旗杆的高度为16 m.