题目内容
1.已知函数y=(m+1)${x}^{{m}^{2}-5}$是反比例函数,且图象在第二、四象限内,则m的值是-2.分析 根据反比例函数的定义得出m2-5=-1,再由函数图象在第二、四象限内,可得出m+1<0,两者联立,解方程及不等式即可得出结论.
解答 解:依题意得:$\left\{\begin{array}{l}{{m}^{2}-5=-1}\\{m+1<0}\end{array}\right.$,
解得:m=-2.
故答案为:-2.
点评 本题考查了反比例函数的定义、反比例函数的性质、解一元二次方程以及解一元一次不等式,解题的关键是得出关于m的一元二次方程和一元一次不等式.本题属于基础题,难度不大,解决该题型题目时,根据反比例函数的定义得出方程,根据反比例函数的性质得出不等式,解方程及不等式即可得出结论.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
14.马大哈做题很快,但经常不仔细思考,所以往往错误率很高,有一次做了四个题,但只做对了一个,他做对的是( )
| A. | a8÷a4=a2 | B. | a3•a4=a12 | C. | $\sqrt{4}$=±2 | D. | 2x3•x2=2x5 |
15.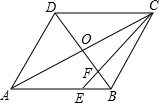 如图,在?ABCD中,AC与BD交于点O,E为AB上一点,且AE=2EB,连接CE交BD于点F,则S△BEF与S△COF的比值为( )
如图,在?ABCD中,AC与BD交于点O,E为AB上一点,且AE=2EB,连接CE交BD于点F,则S△BEF与S△COF的比值为( )
 如图,在?ABCD中,AC与BD交于点O,E为AB上一点,且AE=2EB,连接CE交BD于点F,则S△BEF与S△COF的比值为( )
如图,在?ABCD中,AC与BD交于点O,E为AB上一点,且AE=2EB,连接CE交BD于点F,则S△BEF与S△COF的比值为( )| A. | 1:3 | B. | 1:2 | C. | 2:3 | D. | 3:4 |
16.对与3+$\sqrt{3}$的运算结果的估计正确的是( )
| A. | 1<3+$\sqrt{3}$<2 | B. | 2<3+$\sqrt{3}$<3 | C. | 3<3+$\sqrt{3}$<4 | D. | 4<3+$\sqrt{3}$<5 |
6.$\sqrt{16}$的算术平方根是( )
| A. | 4和-4 | B. | 2和-2 | C. | 4 | D. | 2 |
13.在下列调查中,适宜采用全面调查的是( )
| A. | 了解我省中学生视力情况 | |
| B. | 了解八(1)班学生校服的尺码情况 | |
| C. | 检测一批电灯泡的使用寿命 | |
| D. | 调查石家庄对《新闻联播》栏目的收视率 |
10.一组数$\frac{2}{3}$,$\frac{4}{5}$,$\frac{6}{7}$,$\frac{8}{9}$…按一定的规律排列着,请你根据排列规律,推测这组数的第10个数应为( )
| A. | $\frac{18}{19}$ | B. | $\frac{20}{21}$ | C. | $\frac{22}{23}$ | D. | $\frac{24}{25}$ |
11. 长方体敞口玻璃罐,长、宽、高分别为16cm、6cm和6cm,在罐内点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外壁,在长方形ABCD中心的正上方2cm处,则蚂蚁到达饼干的最短距离是多少cm.( )
长方体敞口玻璃罐,长、宽、高分别为16cm、6cm和6cm,在罐内点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外壁,在长方形ABCD中心的正上方2cm处,则蚂蚁到达饼干的最短距离是多少cm.( )
 长方体敞口玻璃罐,长、宽、高分别为16cm、6cm和6cm,在罐内点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外壁,在长方形ABCD中心的正上方2cm处,则蚂蚁到达饼干的最短距离是多少cm.( )
长方体敞口玻璃罐,长、宽、高分别为16cm、6cm和6cm,在罐内点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外壁,在长方形ABCD中心的正上方2cm处,则蚂蚁到达饼干的最短距离是多少cm.( )| A. | 7$\sqrt{5}$ | B. | $\sqrt{233}$ | C. | 24 | D. | $\sqrt{232}$ |
 用5个完全相同的小正方体组成如图所示的立体图形,它的俯视图是( )
用5个完全相同的小正方体组成如图所示的立体图形,它的俯视图是( )


