题目内容
12.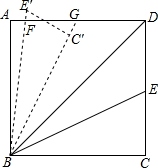 如图,在矩形ABCD中,AB=4$\sqrt{6}$,AD=10.连接BD,∠DBC的角平分线BE交DC于点E,现把△BCE绕点B逆时针旋转,记旋转后的△BCE为△BC′E′.当射线BE′和射线BC′都与线段AD相交时,设交点分别为F,G.若△BFD为等腰三角形,则线段DG长为$\frac{98}{17}$.
如图,在矩形ABCD中,AB=4$\sqrt{6}$,AD=10.连接BD,∠DBC的角平分线BE交DC于点E,现把△BCE绕点B逆时针旋转,记旋转后的△BCE为△BC′E′.当射线BE′和射线BC′都与线段AD相交时,设交点分别为F,G.若△BFD为等腰三角形,则线段DG长为$\frac{98}{17}$.
分析 根据角平分线的性质,寻找等角,等角对等边,构造相似三角形,利用对应线段成比例,即可得答案.
解答  解:在Rt△ABD中,由勾股定理,得
解:在Rt△ABD中,由勾股定理,得
BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{(4\sqrt{6})^{2}+1{0}^{2}}$=14,
在Rt△ABF中,由勾股定理,得:
BF2=(4$\sqrt{6}$)2+(10-BF)2,
解得BF=$\frac{49}{5}$,
AF=10-$\frac{49}{5}$=$\frac{1}{5}$.
过G作GH∥BF,交BD于H,
∴∠FBD=∠GHD,∠BGH=∠FBG,
∵FB=FD,
∴∠FBD=∠FDB,
∴∠FDB=∠GHD,
∴GH=GD,
∵∠FBG=∠EBC=$\frac{1}{2}$∠DBC=$\frac{1}{2}$∠ADB=$\frac{1}{2}$∠FBD,
又∵∠FBG=∠BGH,∠FBG=∠GBH,
∴BH=GH,
设DG=GH=BH=x,则FG=FD-GD=$\frac{49}{5}$-x,HD=14-x,
∵GH∥FB,
∴$\frac{FD}{GD}=\frac{BD}{HD}$,即$\frac{\frac{49}{5}}{x}=\frac{14}{14-x}$,
解得x=$\frac{98}{17}$.
故答案为:$\frac{98}{17}$.
点评 本题考查了旋转的性质,利用了勾股定理,旋转的性质,正切函数的定义是解题关键.

练习册系列答案
相关题目
2.下列亊件中,不可能亊件是( )
| A. | 掷一枚六个面分别刻有1~6数码的均匀正方体骰子,向上一面的点数是“5” | |
| B. | 任意选择某个电视频道,正在播放动画片 | |
| C. | 在平面内,度量一个三角形的内角度数,其和为360° | |
| D. | 肥皂泡会破碎 |
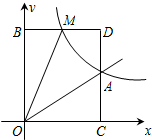 已知反比例函数$y=\frac{k}{x}$的图象经过点A(2,1).点M(m,n)(0<m<2)是该函数图象上的一动点,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.
已知反比例函数$y=\frac{k}{x}$的图象经过点A(2,1).点M(m,n)(0<m<2)是该函数图象上的一动点,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.