题目内容
4.在△ABC中,∠ABC=90°,AB=4,BC=3,若⊙O和三角形三边所在直线都相切,则符合条件的⊙O的半径为1,2,3,6.分析 首先利用勾股定理求得斜边BC的长,根据直角三角形三边的长和内切圆的半径之间的关系求解即可.
解答 解:设圆的半径为r,
①如图,当是圆O时,∵在△ABC中,∠ABC=90°,AB=4,BC=3,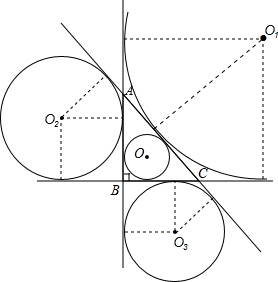
∴斜边AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5,
则符合条件的⊙O的半径为:r=$\frac{3+4-5}{2}$=1,
②当是⊙O1时,⊙01的半径为$\frac{5+3+4}{2}$=6,
③当是⊙O2时,根据切线长定理得:4-r+5=3+r,
解得:r=3,
④当是⊙O3时,根据切线长定理得:3-r+5=4+r,
解得:r=2,
故答案是:1,2,3,6.
点评 本题考查了直角三角形的内切圆,切线长定理,勾股定理的应用,能求出符合条件的所有情况是解此题的关键,注意:直角三角形的三边分别是a、b、c,其中c是斜边,则内切圆的半径是$\frac{a+b-c}{2}$.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
15.下列计算结果是负数的是( )
| A. | 3-2 | B. | 3×(-2) | C. | 3-2 | D. | $\sqrt{3}$ |
19. 如图,已知直线a∥b,直线c与a,b分别交于A,B,且∠1=110°,则∠2=( )
如图,已知直线a∥b,直线c与a,b分别交于A,B,且∠1=110°,则∠2=( )
 如图,已知直线a∥b,直线c与a,b分别交于A,B,且∠1=110°,则∠2=( )
如图,已知直线a∥b,直线c与a,b分别交于A,B,且∠1=110°,则∠2=( )| A. | 70° | B. | 110° | C. | 30° | D. | 150° |
9. 将如图所示的几何图形,绕直线l旋转一周得到的立体图形( )
将如图所示的几何图形,绕直线l旋转一周得到的立体图形( )
 将如图所示的几何图形,绕直线l旋转一周得到的立体图形( )
将如图所示的几何图形,绕直线l旋转一周得到的立体图形( )| A. |  | B. |  | C. |  | D. |  |
16.如图,点O是圆形纸片的圆心,将这个圆形纸片按下列顺序折叠,使$\widehat{AB}$和$\widehat{AC}$都经过圆心O,则阴影部分的面积是⊙O面积的( )
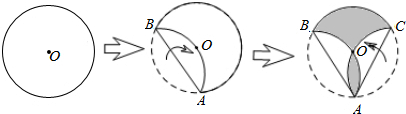

| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{5}$ |
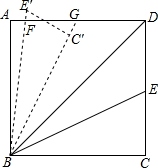 如图,在矩形ABCD中,AB=4$\sqrt{6}$,AD=10.连接BD,∠DBC的角平分线BE交DC于点E,现把△BCE绕点B逆时针旋转,记旋转后的△BCE为△BC′E′.当射线BE′和射线BC′都与线段AD相交时,设交点分别为F,G.若△BFD为等腰三角形,则线段DG长为$\frac{98}{17}$.
如图,在矩形ABCD中,AB=4$\sqrt{6}$,AD=10.连接BD,∠DBC的角平分线BE交DC于点E,现把△BCE绕点B逆时针旋转,记旋转后的△BCE为△BC′E′.当射线BE′和射线BC′都与线段AD相交时,设交点分别为F,G.若△BFD为等腰三角形,则线段DG长为$\frac{98}{17}$.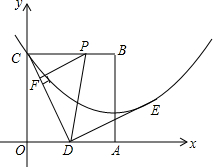 边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.
边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.