题目内容
3.($\frac{1}{2}$)-2-20150+$\sqrt{32}$÷$\sqrt{2}$-2sin45°.分析 分别根据负指数幂的计算法则、0指数幂的运算法则、二次根式的性质性质、特殊角的函数值分别计算出各数,再根据实数混合运算的法则进行计算即可.
解答 解:原式=22-1+4$\sqrt{2}$÷$\sqrt{2}-$2×$\frac{\sqrt{2}}{2}$
=4-1+4-$\sqrt{2}$
=-1-$\sqrt{2}$.
点评 本题考查的是实数的运算,熟知0指数幂的计算法则、二次根式的性质的性质、负指数幂的运算法则、45°角的正弦值是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.顺次连接下面四边形各边中点,得到的四边形一定是正方形的是( )
| A. | 正方形 | B. | 菱形 | C. | 矩形 | D. | 平行四边形 |
11.某商场新近一批A、B两种型号的节能防近视台灯,每台进价分别为200元、170元,近两周的销售情况如下:
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的台灯的销售单价;
(2)若该商场准备用不多于5400元的金额再购进这两种型号的台灯共30台,求A种型号的台灯最多能购进多少台?
(3)在(2)的条件下,该商场销售完这30台台灯能否实现利润为1400元的目标,若能,请给出相应的采购方案;若不能,请说明理由.
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 1800元 |
| 第二周 | 4台 | 10台 | 3100元 |
(1)求A、B两种型号的台灯的销售单价;
(2)若该商场准备用不多于5400元的金额再购进这两种型号的台灯共30台,求A种型号的台灯最多能购进多少台?
(3)在(2)的条件下,该商场销售完这30台台灯能否实现利润为1400元的目标,若能,请给出相应的采购方案;若不能,请说明理由.
15.下列计算结果是负数的是( )
| A. | 3-2 | B. | 3×(-2) | C. | 3-2 | D. | $\sqrt{3}$ |
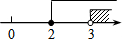
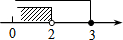

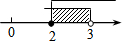




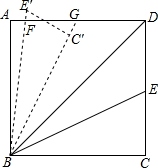 如图,在矩形ABCD中,AB=4$\sqrt{6}$,AD=10.连接BD,∠DBC的角平分线BE交DC于点E,现把△BCE绕点B逆时针旋转,记旋转后的△BCE为△BC′E′.当射线BE′和射线BC′都与线段AD相交时,设交点分别为F,G.若△BFD为等腰三角形,则线段DG长为$\frac{98}{17}$.
如图,在矩形ABCD中,AB=4$\sqrt{6}$,AD=10.连接BD,∠DBC的角平分线BE交DC于点E,现把△BCE绕点B逆时针旋转,记旋转后的△BCE为△BC′E′.当射线BE′和射线BC′都与线段AD相交时,设交点分别为F,G.若△BFD为等腰三角形,则线段DG长为$\frac{98}{17}$.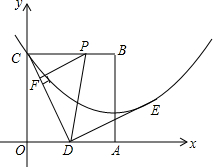 边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.
边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.