题目内容
2.在以O为圆心3cm为半径的圆周上,依次有A、B、C三个点,若四边形OABC为菱形,则该菱形的边长等于3cm;弦AC所对的弧长等于2π或4πcm.分析 连接OB和AC交于点D,根据菱形及直角三角形的性质先求出AC的长及∠AOC的度数,然后求出∠AOC,根据弧长公式的计算计算即可.
解答 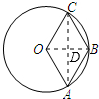 解:连接OB和AC交于点D,
解:连接OB和AC交于点D,
∵四边形OABC为菱形,
∴OA=AB=BC=OC,
∵⊙O半径为3cm,
∴OA=OC=3cm,
∵OA=OB,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴∠AOC=120°,
∴$\widehat{AC}$=$\frac{120•π×3}{180}$=2π,
∴优弧$\widehat{AC}$=$\frac{240π×3}{180}$=4π,
故答案为3,2π或4π.
点评 本题考查了弧长的计算,菱形的性质,等边三角形的判定和性质,解题关键是熟练掌握弧长公式l=$\frac{nπr}{180}$,有一定的难度.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
10.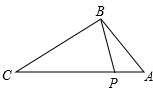 如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
 如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )| A. | ∠ABP=∠C | B. | ∠APB=∠ABC | C. | $\frac{AP}{AB}$=$\frac{AB}{AC}$ | D. | $\frac{AB}{BP}$=$\frac{AC}{CB}$ |
7. 如图是二次函数y=ax2+bx+c的图象,下列结论:
如图是二次函数y=ax2+bx+c的图象,下列结论:
①二次三项式ax2+bx+c的最大值为4;
②4a+2b+c<0;
③一元二次方程ax2+bx+c=1的两根之和为-1;
④使y≤3成立的x的取值范围是x≥0.
其中正确的个数有( )
 如图是二次函数y=ax2+bx+c的图象,下列结论:
如图是二次函数y=ax2+bx+c的图象,下列结论:①二次三项式ax2+bx+c的最大值为4;
②4a+2b+c<0;
③一元二次方程ax2+bx+c=1的两根之和为-1;
④使y≤3成立的x的取值范围是x≥0.
其中正确的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.下列运算正确( )
| A. | a•a5=a5 | B. | a7÷a5=a3 | C. | (2a)3=6a3 | D. | 10ab3÷(-5ab)=-2b2 |
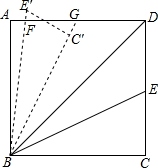 如图,在矩形ABCD中,AB=4$\sqrt{6}$,AD=10.连接BD,∠DBC的角平分线BE交DC于点E,现把△BCE绕点B逆时针旋转,记旋转后的△BCE为△BC′E′.当射线BE′和射线BC′都与线段AD相交时,设交点分别为F,G.若△BFD为等腰三角形,则线段DG长为$\frac{98}{17}$.
如图,在矩形ABCD中,AB=4$\sqrt{6}$,AD=10.连接BD,∠DBC的角平分线BE交DC于点E,现把△BCE绕点B逆时针旋转,记旋转后的△BCE为△BC′E′.当射线BE′和射线BC′都与线段AD相交时,设交点分别为F,G.若△BFD为等腰三角形,则线段DG长为$\frac{98}{17}$.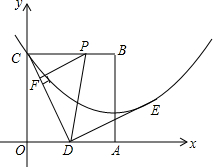 边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.
边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点. 如图,四边形ABCD、BEFG均为正方形,连接AG、CE.
如图,四边形ABCD、BEFG均为正方形,连接AG、CE.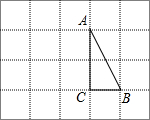 如图,在边长为1的小正方形组成的方格纸上,分别将△ABC向左平移3个单位和绕着点A顺时针旋转90°.
如图,在边长为1的小正方形组成的方格纸上,分别将△ABC向左平移3个单位和绕着点A顺时针旋转90°.