题目内容
1．一个三角形的三边长分别为4，5，6，则连结各边中点所得三角形的周长为$\frac{15}{2}$．分析 根据三角形的中位线定理“三角形的中位线等于第三边的一半”，易得连接这个三角形三边中点所得的三角形的三边是此三角形的三条中位线，即可得知所得的三角形的周长是原三角形周长的一半．
解答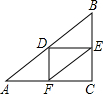 
解：如图，∵D，E，F分别是△ABC的三边的中点，
∴DE=$\frac{1}{2}$AC，DF=$\frac{1}{2}$BC，EF=$\frac{1}{2}$AB，
∴△DEF的周长=DE+DF+EF=$\frac{1}{2}$（AC+BC+AB）=$\frac{1}{2}$×（4+5+6）=$\frac{15}{2}$．
故答案是：$\frac{15}{2}$．
点评 本题考查了三角形的中位线定理：三角形的中位线等于第三边的一半，熟练掌握三角形的中位线定理是解题的关键．
练习册系列答案
相关题目
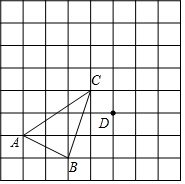在正方形网格中，每个小正方形的边长都为1个单位长度，△ABC的三个顶点的位置如图所示，现将△ABC平移后得△DEF，使点A的对应点为点D，点B的对应点为点E．
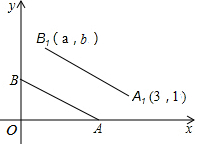如图所示，A、B的坐标分别为（2，0），（0，1），且线段A1B1=AB，A1B1∥AB．若A1、B1的坐标分别为（3，1），（a，b），则a+b的值为（ ）