题目内容
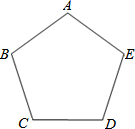 如图,甲、乙两人想在正五边形ABCDE内部找一点P,使得四边形ABPE为平行四边形,其作法如下:
如图,甲、乙两人想在正五边形ABCDE内部找一点P,使得四边形ABPE为平行四边形,其作法如下:学生甲:连结BD、CE,两线段相交于P点,则P即为所求;
学生乙:先取CD的中点M,再以A为圆心,AB长为半径画弧,交AM于P点,则P即为所求.对于学生甲、乙两人的作法,你认为谁的作法正确,并说明正确的理由.
考点:平行四边形的判定
专题:
分析:求出五边形的每个角的度数,求出∠ABP、∠AEP、∠BPE的度数,根据平行四边形的判定判断即可.
解答:解:甲的作法正确,
理由如下:
∵正五边形的每个内角的度数是108°,AB=BC=CD=DE=AE,
∴∠DEC=∠DCE=
×(180°-108°)=36°,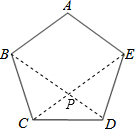
同理∠CBD=∠CDB=36°,
∴∠ABP=∠AEP=108°-36°=72°,
∴∠ABP+∠A=180°,∠AEP+∠A=180°,
∴BP∥AE,AB∥PE,
∴四边形ABPE是平行四边形,即甲正确.
理由如下:
∵正五边形的每个内角的度数是108°,AB=BC=CD=DE=AE,
∴∠DEC=∠DCE=
| 1 |
| 2 |

同理∠CBD=∠CDB=36°,
∴∠ABP=∠AEP=108°-36°=72°,
∴∠ABP+∠A=180°,∠AEP+∠A=180°,
∴BP∥AE,AB∥PE,
∴四边形ABPE是平行四边形,即甲正确.
点评:本题考查了正五边形的内角和定理,等腰三角形的性质,三角形的内角和定理,平行四边形的判定的应用,注意:有两组对角分别相等的四边形是平行四边形.

练习册系列答案
相关题目
下列运算正确的是( )
| A、3a2-a=2a |
| B、(-a3)2=a5 |
| C、a6÷a4=a2 |
| D、(a-b)2=a2-b2 |
 如图:已知正方形OABC的边OC、OA分别在x轴和y轴的正半轴上,点B坐标为(4,4).二次函数y=
如图:已知正方形OABC的边OC、OA分别在x轴和y轴的正半轴上,点B坐标为(4,4).二次函数y=
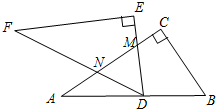 如图,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,如图,将△DEF绕点D旋转,点D与AB的中点重合,DE,DF分别交AC于点M,N,使DM=MN,则重叠部分(△DMN)的面积为
如图,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,如图,将△DEF绕点D旋转,点D与AB的中点重合,DE,DF分别交AC于点M,N,使DM=MN,则重叠部分(△DMN)的面积为