题目内容
 如图:已知正方形OABC的边OC、OA分别在x轴和y轴的正半轴上,点B坐标为(4,4).二次函数y=-
如图:已知正方形OABC的边OC、OA分别在x轴和y轴的正半轴上,点B坐标为(4,4).二次函数y=-| 1 |
| 6 |
(1)求b、c的值及点E和点F的坐标;
(2)当点P在线段OC上时,求证:OP=CD;
(3)在点P运动过程中,当△AOP与以A、B、D为顶点的三角形相似时,求点P的坐标;
(4)在点P运动到OC中点时,能否将△AOP绕平面内某点旋转90°后使得△AOP的两个顶点落在x轴上方的抛物线上?若能,请直接写出旋转中心M的坐标;若不能,请说明理由.
考点:二次函数综合题
专题:
分析:(1)根据正方形的性质求出点A的坐标,然后把点A、B的坐标代入函数解析式求出b、c,即可得解;
(2)表示出PO、PC,再根据同角的余角相等求出∠OAP=∠CPG,然后求出△AOP和△PCG全等,再根据全等三角形对应边相等即可求得;
(3)分三种情况分别讨论,①当P点在线段OC上,因为OA=AB,△AOP与以A、B、D为顶点的三角形相似时,则这两个三角形全等,求得OP=BD.②点P在线段CF上,通过△AOP与三角形DBA相似,以及△AOP与△OCD全等即可求得;③点P在线段OE上通过△AOP与三角形DBA相似,以及△AOP与△OCD全等即可求得.
(4)设O′的坐标为(x,y),则P′(x,y-2),A′(x+4,y),然后将P′、A′代入抛物线的解析式,求得x、y的值,最后通过三角形O′MG与三角形MQH全等即可求得.
(2)表示出PO、PC,再根据同角的余角相等求出∠OAP=∠CPG,然后求出△AOP和△PCG全等,再根据全等三角形对应边相等即可求得;
(3)分三种情况分别讨论,①当P点在线段OC上,因为OA=AB,△AOP与以A、B、D为顶点的三角形相似时,则这两个三角形全等,求得OP=BD.②点P在线段CF上,通过△AOP与三角形DBA相似,以及△AOP与△OCD全等即可求得;③点P在线段OE上通过△AOP与三角形DBA相似,以及△AOP与△OCD全等即可求得.
(4)设O′的坐标为(x,y),则P′(x,y-2),A′(x+4,y),然后将P′、A′代入抛物线的解析式,求得x、y的值,最后通过三角形O′MG与三角形MQH全等即可求得.
解答:(1)解:把(0,4),(4,4)分别代入y=-
x2+bx+c中,
得
,
解得
;
令y=0得-
x2+
x+4=0,
∴x1=2
+2,x2=-2
+2;
∴E(-2
+2,0),F(2
+2,0)
(2)证明:∵正方形OABC,
∴OA=OC,∠AOP=∠OCD=90°,
∴∠OAP+∠APO=90°,
∵OH⊥AP,
∴∠COD+∠APO=90°,
∴∠OAP=∠COD,
在△AOP与△OCD中
,
∴△AOP≌△OCD(AAS),
∴OP=CD.
(3)解:设P(t,0)①当P点在线段OC上时,如原图所示;
∵∠OAP<45°,∠BAD<45°
∵若△AOP∽△ABD,AO=AB,
∴OP=BD,
∴OP=BD=CD=2,
∴t=2
∴P1(2,0).
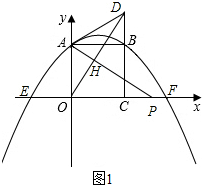
②点P在线段CF上时,如图1所示:
∵∠ADB>∠ODC,
∵∠APO=∠ODC,
∴∠ABD>∠APO,
∴若△AOP∽△ABD,则
=
,
在△AOP与△OCD中
∴△AOP≌△OCD(AAS),
∴OP=CD,
∴DB=PC=t-4,
∴
=
,
解得t=2-2
(舍去)或t=2+2
,
∴P2(2+2
,0).
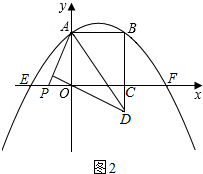
③点P在线段OE上时,如图2所示;
∵∠COD+∠ODC=90°,∠HOP+∠APO=90°,∠COD=∠HOP,
∴∠ODC=∠APO,
∵∠ODC>∠ADB,
∴∠APO>∠ADB,
∴若△AOP∽△ABD,则
=
,
在△AOP与△OCD中
∴△AOP≌△OCD(AAS),
∴OP=CD,
∴DB=PC=4-t,
∴
=
,
解得t=2+2
(舍去)或t=2-2
,
∴P3(2-2
,0).
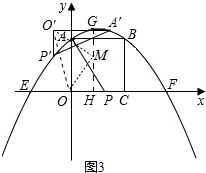
(4)(2,2),(1
,3
),(-
,
);
解:如图3所示:设△AOP绕点M顺时针旋转90°得到△A′O′P′,且P′、A′两点在抛物线y=-
x2+
x+4上,
设O′(x,y),则P′(x,y-2),A′(x+4,y)
∴
,
解得
,
作MG⊥O′A′于G,MH⊥OC于H,设M(a,b),
∵△O′MG≌△MOH,
∴O′G=MH=b,MG=OH=a,
∴
,
解得
,
∴M(1
,3
).
| 1 |
| 6 |
得
|
解得
|
令y=0得-
| 1 |
| 6 |
| 2 |
| 3 |
∴x1=2
| 7 |
| 7 |
∴E(-2
| 7 |
| 7 |
(2)证明:∵正方形OABC,
∴OA=OC,∠AOP=∠OCD=90°,
∴∠OAP+∠APO=90°,
∵OH⊥AP,
∴∠COD+∠APO=90°,
∴∠OAP=∠COD,
在△AOP与△OCD中
|
∴△AOP≌△OCD(AAS),
∴OP=CD.
(3)解:设P(t,0)①当P点在线段OC上时,如原图所示;
∵∠OAP<45°,∠BAD<45°
∵若△AOP∽△ABD,AO=AB,
∴OP=BD,
∴OP=BD=CD=2,
∴t=2
∴P1(2,0).

②点P在线段CF上时,如图1所示:
∵∠ADB>∠ODC,
∵∠APO=∠ODC,
∴∠ABD>∠APO,
∴若△AOP∽△ABD,则
| AO |
| DB |
| OP |
| AB |
在△AOP与△OCD中
|
∴△AOP≌△OCD(AAS),
∴OP=CD,
∴DB=PC=t-4,
∴
| 4 |
| t-4 |
| t |
| 4 |
解得t=2-2
| 5 |
| 5 |
∴P2(2+2
| 5 |

③点P在线段OE上时,如图2所示;
∵∠COD+∠ODC=90°,∠HOP+∠APO=90°,∠COD=∠HOP,
∴∠ODC=∠APO,
∵∠ODC>∠ADB,
∴∠APO>∠ADB,
∴若△AOP∽△ABD,则
| AO |
| DB |
| OP |
| AB |
在△AOP与△OCD中
|
∴△AOP≌△OCD(AAS),
∴OP=CD,
∴DB=PC=4-t,
∴
| 4 |
| 4-t |
| -t |
| 4 |
解得t=2+2
| 5 |
| 5 |
∴P3(2-2
| 5 |

(4)(2,2),(1
| 9 |
| 16 |
| 1 |
| 16 |
| 1 |
| 16 |
| 41 |
| 16 |
解:如图3所示:设△AOP绕点M顺时针旋转90°得到△A′O′P′,且P′、A′两点在抛物线y=-
| 1 |
| 6 |
| 2 |
| 3 |
设O′(x,y),则P′(x,y-2),A′(x+4,y)
∴
|
解得
|
作MG⊥O′A′于G,MH⊥OC于H,设M(a,b),
∵△O′MG≌△MOH,
∴O′G=MH=b,MG=OH=a,
∴
|
解得
|
∴M(1
| 9 |
| 16 |
| 1 |
| 16 |
点评:本题是二次函数的综合题型,主要应用了待定系数法求二次函数的解析式,相似三角形的性质,全等三角形的判定和性质.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
下列调查方式合适的是( )
| A、了解炮弹的杀伤力,采用普查的方式 |
| B、了解全国中学生的睡眠状况,采用普查的方式 |
| C、了解人们保护水资源的意识,采用抽样调查的方式 |
| D、对载人航天器“神舟六号”零部件的检查,采用抽样调查的方式 |
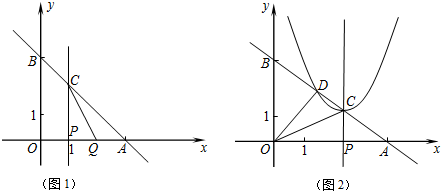
 如图,过点B(2,0)的直线l:y=kx+2
如图,过点B(2,0)的直线l:y=kx+2 如图,在平面直角坐标系xOy中,矩形ABCD的边AB在x轴上,且AB=3,BC=
如图,在平面直角坐标系xOy中,矩形ABCD的边AB在x轴上,且AB=3,BC= 如图,已知A(-2,n)B(3,-2)是一次函数y=kx+b的图象和反比例函数y=
如图,已知A(-2,n)B(3,-2)是一次函数y=kx+b的图象和反比例函数y=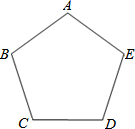 如图,甲、乙两人想在正五边形ABCDE内部找一点P,使得四边形ABPE为平行四边形,其作法如下:
如图,甲、乙两人想在正五边形ABCDE内部找一点P,使得四边形ABPE为平行四边形,其作法如下: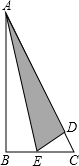 如图所示的三角形纸片中∠B=90°,AC=13,BC=5.现将纸片进行折叠,使得顶点B落在AC边上,折痕为AE.则BE的长为
如图所示的三角形纸片中∠B=90°,AC=13,BC=5.现将纸片进行折叠,使得顶点B落在AC边上,折痕为AE.则BE的长为