题目内容
已知：如图，D是△ABC上一点，E是AC中点，连接DE并延长至F，使EF=DE，连接CF．求证：CF平行且等于DA．考点：全等三角形的判定与性质
专题：证明题
分析：由AE=CE，DE=FE，夹角为对顶角，利用SAS得到三角形AED与三角形CEF全等，利用全等三角形对应边相等得到AD=CF，且得到一对内错角相等，利用内错角相等两直线平行得到CF与AD平行．
解答：证明：在△AED和△CEF中，
，
∴△AED≌△CEF（SAS），
∴AD=CF，∠A=∠ECF，
∴AD∥CF，
则CF平行且等于DA．
|
∴△AED≌△CEF（SAS），
∴AD=CF，∠A=∠ECF，
∴AD∥CF，
则CF平行且等于DA．
点评：此题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解本题的关键．
练习册系列答案
智慧小复习系列答案
相关题目
（1）如图，小红同学用仪器测量一棵大树AB的高度，在C处测得∠ADG=30°，在E处测得∠AFG=60°，CE=8米，仪器高度CD=1.5米，求这棵树AB的高度（结果保留两位有效数字，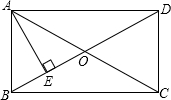
如图，在矩形ABCD中，AE⊥BD于E，且BE：ED=1：3，求证：AC=2AB．
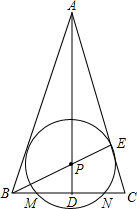已知△ABC，AB=AC，∠BAC=30°，AD⊥BC于D，E在AC上，BE=BC，BC=2
如图，在梯形ABCD中，AB∥DC，DE∥CB，梯形的周长为28，△ADE周长为20，则DC=